783. Докажите, что сумма квадратов расстояний от точки, лежащей на окружности, до вершин правильного вписанного в эту окружность треугольника есть величина постоянная, не зависящая от положения точки на окружности.
Указание. Если M
— точка, лежащая на меньшей дуге AB
окружности, описанной около равностороннего треугольника ABC
, то CM=AM+BM
.
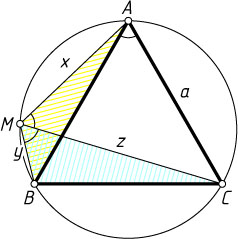
Решение. Пусть M
— произвольная точка меньшей дуги AB
окружности, описанной около равностороннего треугольника ABC
. Обозначим
AM=x,~CM=z,~BM=y,~AB=BC=AC=a.
Воспользуемся известным равенством: CM=AM+BM
(см. задачу 17), или z=x+y
.
Поскольку \angle AMC=\angle BMC=60^{\circ}
, а \angle AMB=120^{\circ}
, то по теореме косинусов из треугольника AMB
находим, что
x^{2}+y^{2}+xy=a^{2},~\mbox{или}~x^{2}+y(x+y)=a^{2}.
Поскольку x+y=z
, то x^{2}+yz=a^{2}
.
По теореме косинусов из треугольника CMB
находим, что
z^{2}+y^{2}-zy=a^{2}.
Подставив вместо zy
в это равенство a^{2}-x^{2}
, получим:
z^{2}+y^{2}+x^{2}=2a^{2}.
Это значит, что сумма квадратов расстояний от любой точки окружности до вершин треугольника ABC
равна одной и той же величине 2a^{2}
.
Источник: Вступительный экзамен в МФТИ. — 1954, билет 12, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 54-12-1, с. 48
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 469, с. 73
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 38, с. 8