808. В параллелограмме ABCD
опустили перпендикуляр BH
на сторону AD
. На отрезке BH
отметили точку M
, равноудалённую от точек C
и D
. Пусть точка K
— середина стороны AB
. Докажите, что угол MKD
прямой.
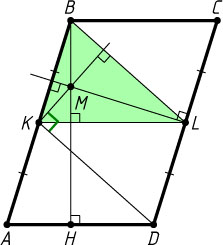
Решение. Первый способ. Пусть L
— середина стороны CD
(рис. 1). Тогда LM
— серединный перпендикуляр к стороне CD
, а так как AB\parallel CD
, то LM\perp BK
. С другой стороны, KL\parallel AD
и BH\perp AD
, поэтому BM\perp KL
. Следовательно, M
— точка пересечения высот треугольника BKL
, проведённых из вершин L
и B
, а так как высоты треугольника пересекаются в одной точке и KD\parallel BL
, то KM\perp BL
, а значит, KM\perp KD
. Что и требовалось доказать.
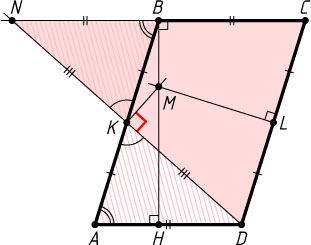
Второй способ. Пусть L
— середина стороны CD
, N
— точка пересечения прямых DK
и BC
(рис. 2). Треугольники BKN
и AKD
равны по стороне и двум прилежащим к ней углам, поэтому BN=AD=BC
, т. е. B
— середина стороны CN
треугольника CND
, а BH
— серединный перпендикуляр к CN
. С другой стороны, прямая LM
— серединный перпендикуляр к стороне CD
этого треугольника, а так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и K
— середина стороны DN
, то KM
— серединный перпендикуляр к стороне DN
. Следовательно, KM\perp KD
. Что и требовалось доказать.
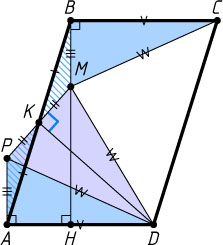
Третий способ. Пусть P
— точка, симметричная точке M
относительно середины K
стороны AB
(рис. 3). Тогда треугольники AKP
и BKM
равны по двум сторонам и углу между ними, поэтому AP=BM
и PK=KM
.
Прямоугольные треугольники APD
и BMC
равны по двум катетам, поэтому PD=MC=MD
. Значит, треугольник MDP
равнобедренный, поэтому его медиана DK
является высотой. Следовательно, \angle MKD=90^{\circ}
.
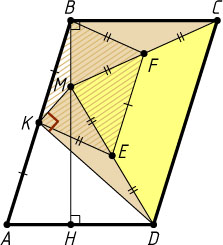
Четвёртый способ. Пусть F
и E
— середины отрезков CM
и DM
соответственно (рис. 4). Тогда EF
— средняя линия треугольника CMD
, поэтому EF=\frac{1}{2}CD=\frac{1}{2}AB=BK
и EF\parallel CD\parallel BK
, значит, BFEK
— параллелограмм. Тогда KE\parallel BF
и KE=BF
.
Отрезок BF
— медиана прямоугольного треугольника BMC
, проведённая из вершины прямого угла, поэтому KE=BF=\frac{1}{2}CM=\frac{1}{2}DM
. Медиана KE
треугольника DKM
равна половине стороны, к которой она проведена, следовательно, \angle DKM=90^{\circ}
(см. задачу 1188).
Автор: Волчкевич М. А.
Источник: Московская математическая олимпиада. — 2012, LXXV, 8 класс
Источник: Журнал «Квант». — 2012, № 4, с. 51



