818. В прямоугольном треугольнике медиана и высота, проведённые к гипотенузе, равны m
и h
соответственно. Вычислите биссектрису треугольника, проведённую из вершины прямого угла.
Ответ. h\sqrt{\frac{2m}{m+h}}
.
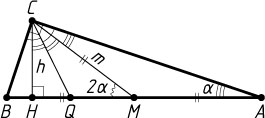
Решение. Пусть CH=h
и CM=m
— высота и медиана прямоугольного треугольника ABC
, проведённые из вершины прямого угла при вершине C
, \angle BCH=\angle CAB=\alpha
. Предположим, что точка H
лежит между B
и M
.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), поэтому \angle ACM=\angle MAC=\alpha
. По теореме о внешнем угле треугольника
\angle CMH=\angle ACM+\angle MAC=2\alpha.
Из прямоугольного треугольника CMH
находим, что \sin2\alpha=\frac{CH}{CM}=\frac{h}{m}
.
Пусть CQ
— искомая биссектриса треугольника ABC
. Тогда
\angle HCQ=45^{\circ}-\angle BCH=45^{\circ}-\alpha.
Из прямоугольного треугольника CHQ
находим, что
CQ=\frac{CH}{\cos\angle HCQ}=\frac{h}{\cos(45^{\circ}-\alpha)},
а так как
\cos(45^{\circ}-\alpha)=\cos45^{\circ}\sin\alpha+\sin45^{\circ}\sin\alpha=\frac{1}{\sqrt{2}}(\sin\alpha+\cos\alpha)=
=\frac{1}{\sqrt{2}}\sqrt{(\sin\alpha+\cos\alpha)^{2}}=\frac{1}{\sqrt{2}}\sqrt{1+\sin2\alpha}=\frac{1}{\sqrt{2}}\sqrt{1+\frac{h}{m}}=\sqrt{\frac{m+h}{2m}},
то
CQ=\frac{h}{\sqrt{\frac{m+h}{2m}}}=h\sqrt{\frac{2m}{m+h}}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 800, с. 99
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.26.1, с. 50
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 48, с. 143
