827. В трапеции ABCD
каждая из диагоналей AC
и BD
равна основанию AB
, M
— середина CD
. Найдите углы трапеции, если \angle MBC=\angle CAB
.
Ответ. 75^{\circ}
, 75^{\circ}
, 105^{\circ}
, 105^{\circ}
.
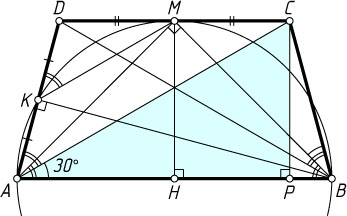
Решение. Первый способ. Диагонали трапеции равны, значит, трапеция — равнобедренная (см. задачу 1915). Пусть K
— середина боковой стороны AD
(рис. 1). Тогда KM
— средняя линия треугольника ADC
, поэтому
\angle DKM=\angle DAC=\angle DBC=\angle MBC+\angle MBD=
=\angle CAB+\angle MBD=\angle ABD+\angle MBD=\angle ABM,
а так как
\angle AKM=180^{\circ}-\angle DKM=180^{\circ}-\angle ABM,
то около четырёхугольника AKMB
можно описать окружность, причём AB
— диаметр этой окружности, поскольку \angle AKB=90^{\circ}
(BK
— высота равнобедренного треугольника ABD
). Значит, \angle AMB=90^{\circ}
. Следовательно, AMB
— равнобедренный прямоугольный треугольник. Его высота MH
равна половине гипотенузы AB
, а значит, и половине AC
.
Пусть CP
— высота трапеции. Тогда CP=MH=\frac{1}{2}AC
. Следовательно,
\angle ABD=\angle CAB=30^{\circ},~\angle ABC=\angle ABM+\angle MBC=45^{\circ}+\angle ABD=45^{\circ}+30^{\circ}=75^{\circ},
\angle BAD=\angle ABC=75^{\circ},~\angle ADC=\angle BCD=180^{\circ}-75^{\circ}=105^{\circ}.
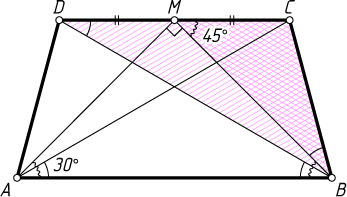
Второй способ. Диагонали трапеции равны, значит, трапеция — равнобедренная. Заметим, что
\angle BDC=\angle ABD=\angle CAB=\angle MBC,
поэтому треугольники BDC
и MBC
подобны по двум углам (рис. 1). Значит, \frac{CD}{BC}=\frac{BC}{CM}
, или
BC^{2}=CD\cdot CM=CD\cdot\frac{1}{2}CD=\frac{1}{2}CD^{2},
поэтому коэффициент подобия треугольников BDC
и MBC
равен \frac{CD}{BC}=\sqrt{2}
. Значит, AB=BD=BM\sqrt{2}=AM\sqrt{2}
. Следовательно, AMB
— равнобедренный прямоугольный треугольник, \angle BAM=\angle ABM=45^{\circ}
.
Применив теорему синусов к треугольнику BMC
, получим, что \frac{CM}{\sin\angle MBC}=\frac{BC}{\sin\angle BMC}
, или \frac{BC\sqrt{2}}{\sin\angle MBC}=\frac{BC}{\sin45^{\circ}}
, откуда \sin\angle MBC=\frac{1}{2}
, а так как \angle MBC\lt90^{\circ}
, то \angle MBC=30^{\circ}
.
Следовательно,
\angle BAD=\angle ABC=\angle ABM+\angle MBC=45^{\circ}+30^{\circ}=75^{\circ},
\angle ADC=\angle BCD=180^{\circ}-75^{\circ}=105^{\circ}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 731, с. 92

