846. Радиус вписанной в треугольник ABC
окружности равен 4, причём AC=BC
. На прямой AB
взята точка D
, удалённая от прямых AC
и BC
на расстояния 11 и 3 соответственно. Найдите косинус угла DBC
.
Ответ. \frac{3}{4}
.
Указание. Через точку D
проведите прямую, параллельную AC
.
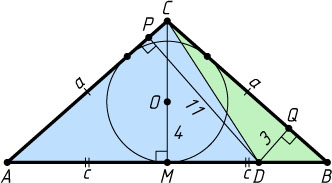
Решение. Первый способ. Пусть CM
— высота треугольника ABC
(рис. 1), P
и Q
— проекции точки D
на прямые AC
и BC
соответственно. Положим AC=BC=a
, AB=2c
.
Если точка D
лежит на отрезке AB
, то
S_{\triangle ABC}=S_{\triangle ADC}+S_{\triangle BDC}=\frac{1}{2}AC\cdot DP+\frac{1}{2}BC\cdot DQ=\frac{1}{2}(11a+3a)=7a.
С другой стороны, поскольку площадь треугольника равна произведению полупериметра на радиус вписанной окружности, то
S_{\triangle ABC}=\frac{1}{2}(a+a+2c)\cdot4=4(a+c).
Из уравнения 7a=4(a+c)
находим, что \frac{c}{a}=\frac{3}{4}
. Следовательно,
\cos\angle DBC=\cos\angle MBC=\frac{BM}{BC}=\frac{c}{a}=\frac{3}{4}.
Если точка D
лежит на продолжении стороны AB
за точку B
, то
S_{\triangle ABC}=S_{\triangle ADC}-S_{\triangle BDC}=\frac{1}{2}AC\cdot DP-\frac{1}{2}BC\cdot DQ=\frac{1}{2}(11a-3a)=4a.
Тогда из уравнения 4a=4(a+c)
следует, что c=0
, что невозможно.
Если точка D
лежит на продолжении стороны AB
за точку A
, то
S_{\triangle ABC}=S_{\triangle BDC}-S_{\triangle ADC}=\frac{1}{2}BC\cdot DQ-\frac{1}{2}AC\cdot DP=\frac{1}{2}(3a-11a)=-4a\lt0,
что также невозможно.
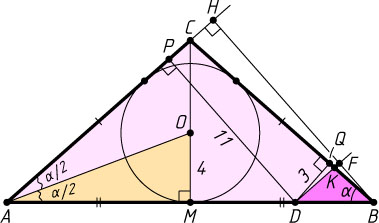
Второй способ. Пусть CM
— высота треугольника ABC
(рис. 2), P
и Q
— проекции точки D
на прямые AC
и BC
соответственно, O
— центр вписанной в треугольник ABC
окружности, \angle CAB=\angle CBA=\alpha
. Тогда
AB=2AM=2OM\ctg\angle OAB=8\ctg\frac{\alpha}{2}=\frac{8(1+\cos\alpha)}{\sin\alpha}.
Проведём через точку D
прямую, параллельную прямой AC
до пересечения с прямой BC
в точке K
. Тогда треугольник BDK
подобен треугольнику BAC
, а так как он равнобедренный, то его высота DQ
равна высоте BF
.
Пусть BH
— высота треугольника ABC
. Если точка D
лежит на продолжении отрезка AB
за точку B
, то
BH=FH-BF=DP-BF=DP-DQ=11-3=8,~AB=\frac{BH}{\sin\angle CAB}=\frac{8}{\sin\alpha}.
Тогда имеем уравнение
\frac{8(1+\cos\alpha)}{\sin\alpha}=\frac{8}{\sin\alpha},
из которого находим, что \cos\alpha=0
, что невозможно.
Если точка D
принадлежит отрезку AB
, то
BH=BF+FH=DQ+DP=11+3=14.
Тогда имеем уравнение
\frac{8(1+\cos\alpha)}{\sin\alpha}=\frac{14}{\sin\alpha},
из которого находим, что \cos\alpha=\frac{3}{4}
.
Очевидно, что точка D
не может лежать на продолжении AB
за точку A
.
Третий способ. Пусть CM
— высота треугольника ABC
, P
и Q
— проекции точки D
на прямые AC
и BC
соответственно, вписанная окружность с центром O
касается боковой стороны AC
треугольника ABC
в точке T
.
Через точку L
, диаметрально противоположную T
, проведём касательную к окружности. Пусть E
, N
и F
— точки пересечения касательной с прямыми AB
, BC
и DP
соответственно. Тогда треугольник BNE
равнобедренный, NO
— биссектриса его внешнего угла при вершине. Значит, NO\parallel AB
(см. задачу 1174),
PF=LT=2OT=8,~DF=DP-PF=11-8=3=DQ,
а так как
\angle DEF=\angle NBE=\angle DBQ,
то прямоугольные треугольники EFD
и BQD
равны по катету и противолежащему острому углу. Тогда ED=BD
.
Если при этом точка D
лежит на продолжении отрезка AB
за точку B
(рис. 3), то равенство ED=BD
невозможно. Если точка D
лежит на отрезке AB
(рис. 4), то D
— середина BE
, а ND
— высота равнобедренного треугольника BNE
. Тогда DN\perp ON
, DNOM
— прямоугольник и
\angle CBA=\angle BDQ=\angle CBA=\angle QDN.
Следовательно,
\cos\angle CBA=\cos\angle QDN=\frac{DQ}{DN}=\frac{DQ}{OM}=\frac{3}{4}.
Очевидно, что точка D
не может лежать на продолжении AB
за точку A
.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1987, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 12

