858. Дана трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно \sqrt{\frac{2}{3}}
. Найдите углы трапеции.
Ответ. 45^{\circ}
, 135^{\circ}
.
Указание. Выразите диагональ трапеции двумя способами: через радиус описанной окружности и острый угол трапеции; через высоту и острый угол трапеции.
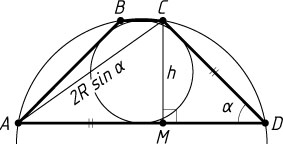
Решение. Первый способ. Пусть \alpha
— острый угол трапеции ABCD
, h
— высота трапеции, R
— радиус описанной окружности, M
— проекция вершины C
меньшего основания BC
на большее основание AD
. Тогда (см. задачу 1921)
AM=\frac{1}{2}(BC+AD)=\frac{1}{2}(AB+CD)=\frac{1}{2}\cdot2CD=CD,
AC=2R\sin\alpha,~AM=CD=\frac{CM}{\sin\alpha},~AM^{2}+MC^{2}=AC^{2},
или
\frac{h^{2}}{\sin^{2}\alpha}+h^{2}=4R^{2}\sin^{2}\alpha.
Поскольку \frac{h}{R}=\sqrt{\frac{2}{3}}
, то
\frac{2}{3}\left(\frac{1}{\sin^{2}\alpha}+1\right)=4\sin^{2}\alpha,~\mbox{или}~6\sin^{4}\alpha-\sin^{2}\alpha-1=0.
Отсюда находим, что \sin^{2}\alpha=\frac{1}{2}
. Следовательно,
\sin\alpha=\frac{1}{\sqrt{2}},~\alpha=45^{\circ}.
Второй способ. Пусть \alpha
— острый угол трапеции ABCD
, \beta
— угол между диагональю трапеции и большим основанием, h
— высота трапеции, R
— радиус описанной окружности, M
— проекция вершины C
меньшего основания BC
на большее основание AD
. Тогда (см. задачу 1921)
AM=\frac{1}{2}(BC+AD)=\frac{1}{2}(AB+CD)=\frac{1}{2}\cdot2CD=CD=AB,
AC=2R\sin\alpha,~h=CM=AC\sin\beta=2R\sin\alpha\sin\beta,
\sqrt{\frac{2}{3}}=\frac{h}{2R}=\frac{CM}{R}=\frac{2R\sin\alpha\sin\beta}{R}=2\sin\alpha\sin\beta.
Из прямоугольных треугольников ABE
и BED
получаем, что
\sin\alpha=\frac{BE}{AB}=\frac{h}{AM}=\frac{h}{DE}=\tg\beta,
а так как 2\sin\alpha\sin\beta=\sqrt{\frac{2}{3}}
, то 2\sin^{2}\beta=\sqrt{\frac{2}{3}}
, или
2-2\cos^{2}\beta=\sqrt{\frac{2}{3}}\cos\beta~\Leftrightarrow~2\cos^{2}\beta+\sqrt{\frac{2}{3}}\cos\beta-2=0.
Условию задачи удовлетворяет положительный корень \cos\beta=\sqrt{\frac{2}{3}}
этого уравнения. Тогда
\sin\alpha=\tg\beta=\sqrt{\frac{1}{\cos^{2}\beta}-1}=\sqrt{\frac{3}{2}-1}=\frac{1}{\sqrt{2}}.
Следовательно,
\angle CDA=\angle BAD=\alpha=45^{\circ},~\angle BCD=\angle CBA=135^{\circ}.
Примечание. См. также статью Я.Суконника и П.Горнштейна «Можно решить проще!», Квант, 1981, N5, с.42-43.
Источник: Вступительный экзамен на физический факультет МГУ. — 1977, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 27
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.36, с. 33
