886. В остроугольном треугольнике ABC
с углом C
, равным 30^{\circ}
, высоты пересекаются в точке M
. Найдите площадь треугольника AMB
, если расстояние от центра окружности, описанной около треугольника ABC
, до сторон BC
и AC
соответственно равны \sqrt{2}
и \frac{\sqrt{3}}{3}
.
Ответ. \frac{\sqrt{6}}{3}
.
Указание. Пусть O
— центр окружности, описанной около треугольника ABC
, P
— проекция точки O
на BC
. Докажите, что AM=2OP
(см. задачу 1257).
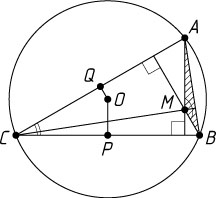
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
, P
и Q
— проекции точки O
на стороны BC
и AC
. Известно, что расстояние от точки пересечения высот треугольника до его вершины вдвое больше расстояния от центра описанной окружности до противоположной стороны треугольника (см. задачу 1257). Поэтому
BM=2OQ=\frac{2\sqrt{3}}{3},~AM=2OP=2\sqrt{2}.
Поскольку \angle AMB=180^{\circ}-30^{\circ}=150^{\circ}
, то
S_{\triangle AMB}=\frac{1}{2}AM\cdot MB\sin150^{\circ}=\frac{\sqrt{6}}{3}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1971, № 5, вариант 6
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.9, с. 122
