1257. Докажите, что расстояние от вершины треугольника до точки пересечения высот вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Указание. Проведите через вершины данного треугольника прямые, параллельные противоположным сторонам. Тогда полученный таким образом треугольник подобен данному с коэффициентом 2.
Решение. Заметим, что для прямоугольного треугольника утверждение очевидно. Рассмотрим случай не прямоугольного треугольника.
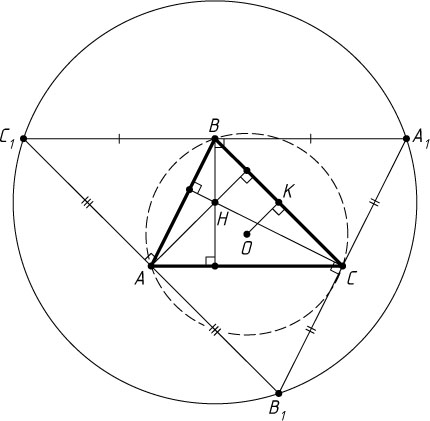
Первый способ. Проведём через вершины данного треугольника ABC
прямые, параллельные противоположным сторонам. Получим новый треугольник, подобный данному с коэффициентом 2 (стороны треугольника ABC
являются средними линиями нового треугольника). При этом высоты треугольника ABC
лежат на серединных перпендикулярах нового треугольника.
Если H
— точка их пересечения, а O
— центр окружности, описанной около треугольника ABC
, то отрезок AH
в новом треугольнике соответствует отрезку OK
(K
— середина BC
) в исходном треугольнике. Поэтому AH=2OK
.
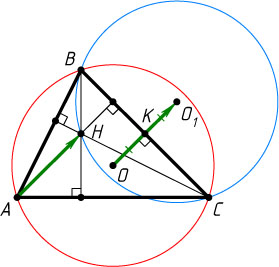
Второй способ. Пусть H
— точка пересечения высот треугольника ABC
. Поскольку \angle BHC=180^{\circ}-\angle A
, то радиусы описанных окружностей треугольников ABC
и HBC
равны (каждый из них равен \frac{BC}{2\sin\angle A}
). Следовательно, эти окружности симметричны относительно прямой BC
.
Если O
и O_{1}
— их центры, то OK=O_{1}K
(K
— середина BC
). С другой стороны, эти окружности переходят друг в друга при параллельном переносе на вектор \overrightarrow{OO_{1}}
(или -\overrightarrow{OO_{1}}
). Следовательно, \overrightarrow{O_{1}O}=\overrightarrow{HA}
. Поэтому HA=O_{1}O=2OK
.
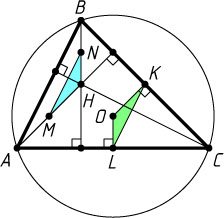
Третий способ. Пусть H
— точка пересечения высот треугольника ABC
; O
— центр его описанной окружности; M
, N
, K
, L
— середины отрезков AH
, BH
, BC
и AC
соответственно. Тогда MN=KL
и MN\parallel KL
(средние линии треугольников ABH
и ABC
), MH\parallel OK
, NH\parallel OL
. Поэтому треугольники MNH
и KLO
равны (по стороне и двум прилежащим к ней углам). Следовательно, OK=MH=\frac{1}{2}AH
.
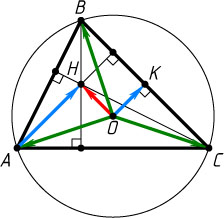
Четвёртый способ. Применив известное векторное равенство \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}
(см. задачу 4516), получим, что
\overrightarrow{OK}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OA})=\frac{1}{2}(\overrightarrow{OH}-\overrightarrow{OA})=\frac{1}{2}\overrightarrow{AH}.
Отсюда следует доказываемое утверждение.
Пятый способ. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр его описанной окружности, A_{1}
— точка, диаметрально противоположная вершине A
.
Тогда \angle ABA_{1}=\angle ACA_{1}=90^{\circ}
, а так как BH\perp AC
и CH\perp AB
, то BH\parallel CA_{1}
и CH\parallel BA_{1}
. Значит, BHCA_{1}
— параллелограмм. Его диагонали делятся точкой пересечения K
пополам. При этом OK\perp BC
.
Отрезок OK
— средняя линия треугольника AHA_{1}
, следовательно, OK=\frac{1}{2}AH
. Что и требовалось доказать.
Шестой способ. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр его описанной окружности; K
, L
и F
— середины отрезков BC
, AC
и CH
соответственно.
Тогда OK\perp BC
и AH\perp BC
, поэтому OK\parallel AH
. С другой стороны, LF
— средняя линия треугольника AHC
, поэтому LF\parallel AH
и LF=\frac{1}{2}AH
. Следовательно, LF\parallel OK
.
Отрезок KF
— средняя линия треугольника BHC
, поэтому KF\parallel BH
, а так как BH\perp AC
, то KF\perp AC
. С другой стороны, OL\perp AC
, значит, OL\parallel KF
.
Противоположные стороны четырёхугольника OKFL
попарно параллельны, значит, это параллелограмм. Следовательно, OK=LF=\frac{1}{2}AH
. Что и требовалось доказать.
Седьмой способ. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр его описанной окружности K
— середина стороны BC
.
Рассмотрим гомотетию с центром в точке пересечения медиан треугольника и коэффициентом -2
. При этой гомотетии середины сторон переходят в вершины, а следовательно, серединные перпендикуляры к сторонам — в высоты. Значит, точка O
переходит в точку H
, а отрезок OK
— в AH
. Следовательно, AH=2OK
.
Примечание. См. также статью Д.Швецова «Важная лемма», Квант, 2012, N5/6, с.57-60.
Источник: Вступительный экзамен в МФТИ. — 1958, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 58-1-3, с. 62
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 117, с. 42
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 30, с. 194
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 20б, с. 7
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 6.2, с. 51



