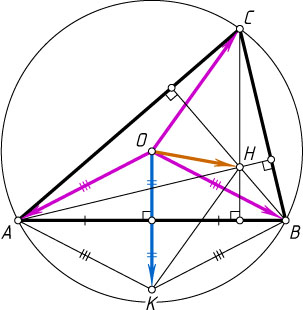
4516. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр описанной окружности. Докажите, что \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}
(Теорема Гамильтона).
Указание. Постройте сначала сумму векторов \overrightarrow{OA}+\overrightarrow{OB}
, а затем прибавьте к ней вектор \overrightarrow{OC}
.
Решение. Рассмотрим сумму векторов \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OK}
. Отрезок OK
— диагональ ромба OAKB
. Поэтому OK\perp AB
. Следовательно, OK\parallel CH
. Тогда, если \overrightarrow{OK}+\overrightarrow{OC}=\overrightarrow{OM}
, то точка M
принадлежит высоте, проходящей через вершину C
.
Таким образом, если \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}_{1}
, то точка H_{1}
принадлежит каждой высоте треугольника ABC
. Следовательно, точки H_{1}
и H
совпадают.
Примечание. 1. Верно и обратное: если O
— центр описанной окружности треугольника ABC
, а точка H
такова, что \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}
, то H
— точка пересечения высот треугольника ABC
(см. задачу 4723).
2. Аналогичное утверждение верно для ортоцентрического тетраэдра: если H
— точка пересечения высот ортоцентрического тетраэдра ABCD
, а O
— центр описанной сферы, то
\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}.
3. См. также статью Э.Г.Готмана «Прямая Эйлера», Квант, 1975, N2, с.20-25.
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 95
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 438(а), с. 68
