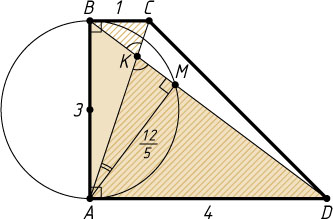
903. Дана трапеция ABCD
, у которой угол BAD
— прямой. На стороне AB
как на диаметре построена окружность, которая пересекает диагональ BD
в точке M
. Известно, что AB=3
, AD=4
, BC=1
. Найдите угол CAM
.
Ответ. \arcsin\frac{1}{\sqrt{10}}
.
Указание. Рассмотрите прямоугольный треугольник AMK
, где K
— точка пересечения диагоналей трапеции.
Решение. Поскольку угол AMB
вписанный и опирается на диаметр AB
, то \angle AMB=90^{\circ}
.
Поскольку AM\cdot BD=AB\cdot AD
(см. задачу 1967), то
AM=\frac{AB\cdot AD}{BD}=\frac{3\cdot4}{5}=\frac{12}{5}.
Пусть K
— точка пересечения диагоналей трапеции. Тогда \frac{AK}{KC}=\frac{AD}{BC}=4
. Поэтому
AK=\frac{4}{5}AC=\frac{4\sqrt{10}}{5}.
Из прямоугольного треугольника AMK
находим, что
\cos\angle KAM=\frac{\frac{12}{5}}{\frac{4\sqrt{10}}{5}}=\frac{3}{\sqrt{10}}.
Следовательно,
\sin\angle CAM=\sin\angle KAM=\frac{1}{\sqrt{10}}.
