908. На стороне AC
остроугольного треугольника ABC
взята точка D
так, что AD=1
, DC=2
, а BD
является высотой треугольника ABC
. Окружность радиуса 2, проходящая через точки A
и D
, касается в точке D
окружности, описанной около треугольника BDC
. Найдите площадь треугольника ABC
.
Ответ. 3\sqrt{15}
.
Указание. Докажите, что окружности касаются внешним образом. Если M
— точка пересечения первой окружности с продолжением BD
, то треугольники ADM
и CDB
подобны.
Решение. Диаметр BC
окружности, описанной около треугольника BDC
, виден из точки A
под острым углом. Поэтому точка A
лежит вне этой окружности (см. задачу 1772). Следовательно, данные окружности касаются внешним образом.
Пусть P
— центр окружности, проходящей через точки A
и D
, M
— точка пересечения продолжения BD
с этой окружностью, O
— центр окружности, описанной около треугольника BDC
. Поскольку
\angle DAM=\angle ADP=\angle ODC=\angle BCD,
то треугольники ADM
и CDB
подобны с коэффициентом \frac{AD}{DC}=\frac{1}{2}
. Следовательно,
BD=2DM=2\sqrt{AM^{2}-AD^{2}}=2\sqrt{16-1}=2\sqrt{15},
S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{3\cdot2\sqrt{15}}{2}=3\sqrt{15}.
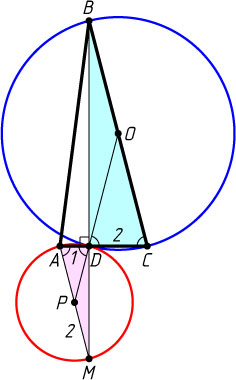
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1974, вариант 1, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 88
