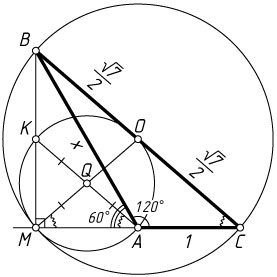
910. В треугольнике ABC
известно, что \angle A=120^{\circ}
, стороны AC=1
и BC=\sqrt{7}
. На продолжении стороны CA
взята точка M
так, что BM
является высотой треугольника ABC
. Найдите радиус окружности, проходящей через точки A
и M
и касающейся в точке M
окружности, проходящей через точки M
, B
и C
.
Ответ. \frac{\sqrt{7}}{4}
.
Указание. Докажите, что окружности касаются внутренним образом. Пусть K
— отличная от M
точка пересечения первой окружности с отрезком BM
. Треугольники MAK
и MCB
подобны.
Решение. Поскольку диаметр BC
окружности, описанной около треугольника MBC
, виден из точки A
под тупым углом, то точка A
лежит внутри этой окружности (см. задачу 1772). Поэтому данные окружности касаются внутренним образом.
Пусть Q
и O
— центры соответственно меньшей и большей окружностей, K
— отличная от M
точка пересечения меньшей окружности с отрезком BM
. Поскольку
\angle MAK=\angle AMQ=\angle CMO=\angle OCM=\angle BCM,
то треугольники MAK
и MCB
подобны.
Обозначим AB=x
и применим к треугольнику ABC
теорему косинусов:
BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos120^{\circ},
или
7=1+x+x^{2},~\mbox{или}~x^{2}+x-6=0.
Отсюда находим, что x=2
, а так как \angle MAB=60^{\circ}
, то
AM=\frac{1}{2}AB=\frac{x}{2}=1.
Следовательно,
AK=BC\cdot\frac{AM}{MC}=\frac{\sqrt{7}}{2},~QA=\frac{1}{2}AK=\frac{\sqrt{7}}{4}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1974, вариант 3, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 88
