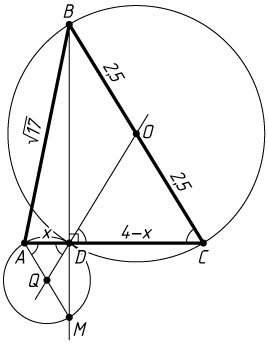
911. Дан треугольник ABC
, у которого стороны AB=\sqrt{17}
, BC=5
, AC=4
. На стороне AC
взята точка D
так, что BD
является высотой треугольника ABC
. Найдите радиус окружности, проходящей через точки A
и D
и касающейся в точке D
окружности, описанной около треугольника BCD
.
Ответ. \frac{5}{6}
.
Указание. Докажите, что окружности касаются внешним образом. Если M
— точка пересечения окружности, проходящей через точки A
и D
, с продолжением BD
, то треугольники ADM
и BCD
подобны.
Решение. Поскольку угол A
острый, точка A
расположена вне окружности, описанной около треугольника BCD
(см. задачу 1772), поэтому указанные окружности касаются внешним образом. Обозначим AD=x
. Тогда CD=AC-x=4-x
.
Поскольку AB^{2}-AD^{2}=BC^{2}-DC^{2}
, то 17-x^{2}=25-(4-x)^{2}
. Отсюда находим, что x=1
.
Пусть M
— точка пересечения окружности, проходящей через точки A
и D
, с продолжением BD
, Q
— центр этой окружности, O
— центр описанной окружности треугольника BCD
. Поскольку
\angle MAD=\angle QAD=\angle ADQ=\angle ODC=\angle OCD=\angle BCD,
то треугольники ADM
и BCD
подобны с коэффициентом \frac{AD}{DC}=\frac{1}{3}
. Следовательно,
AM=\frac{1}{3}BC=\frac{5}{3},~QA=\frac{1}{2}AM=\frac{5}{6}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1974, вариант 4, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 89
