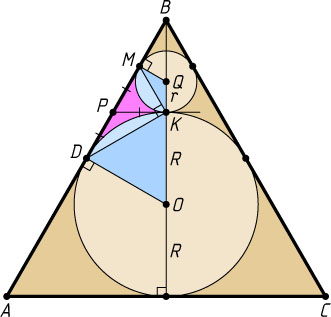
913. В равносторонний треугольник ABC
, сторона которого равна a
, вписана окружность, касающаяся стороны AB
в точке D
. Вторая окружность, расположенная внутри треугольника ABC
, касается внешним образом первой (вписанной) окружности в точке K
, касается стороны AB
в точке M
и стороны BC
. Найдите площадь фигуры DKM
, ограниченной меньшей из дуг DK
, меньшей из дуг KM
и отрезком MD
.
Ответ. \frac{a^{2}(24\sqrt{3}-11\pi)}{648}
.
Указание. Треугольник MKD
— прямоугольный.
Решение. Пусть R
и r
— радиусы данных окружностей (R\gt r
), O
и Q
— их центры, P
— точка пересечения общей касательной, проходящей через точку K
, со стороной AB
. Поскольку PK=PD=PM
, то треугольник MKD
— прямоугольный (см. задачу 1188).
Искомая площадь равна разности площадей треугольника MKD
и двух сегментов. Площадь первого сегмента равна разности площадей сектора DOK
и треугольника DOK
, т. е.
\frac{\pi R^{2}}{6}-\frac{R^{2}\sqrt{3}}{4},
а второго — разности площадей сектора MQK
и треугольника MQK
, т. е.
\frac{\pi r^{2}}{3}-\frac{r^{2}\sqrt{3}}{4}.
Поскольку BK=3R-2R=R
, то r=\frac{1}{3}R
.
Из треугольников MQK
и DOK
находим, что
MK=r\sqrt{3}=\frac{R\sqrt{3}}{3},~DK=R~(R=\frac{a\sqrt{3}}{6}).
Тогда искомая площадь равна
\frac{1}{2}MK\cdot DK-\left(\frac{\pi R^{2}}{6}-\frac{R^{2}\sqrt{3}}{4}\right)-\left(\frac{\pi r^{2}}{3}-\frac{r^{2}\sqrt{3}}{4}\right)=
=\frac{R^{2}\sqrt{3}}{6}-\frac{R^{2}}{2}\left(\frac{\pi}{3}-\frac{\sqrt{3}}{2}\right)-\frac{R^{2}}{9}\left(\frac{\pi}{3}-\frac{\sqrt{3}}{4}\right)=
=\frac{R^{2}(48\sqrt{3}-22\pi)}{108}=\frac{R^{2}(24\sqrt{3}-11\pi)}{54}=\frac{a^{2}(24\sqrt{3}-11\pi)}{648}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1974, вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 60
