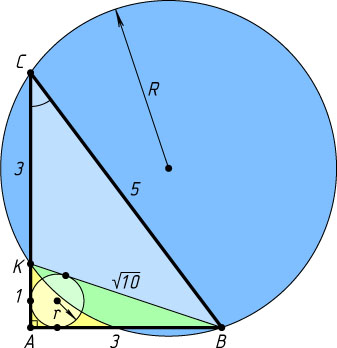
922. В треугольнике ABC
сторона BC
равна 5. Окружность проходит через вершины B
и C
и пересекает сторону AC
в точке K
, причём CK=3
, KA=1
. Известно, что косинус угла ACB
равен \frac{4}{5}
. Найдите отношение радиуса данной окружности к радиусу окружности, вписанной в треугольник ABK
.
Ответ. \frac{25+10\sqrt{10}}{9}
.
Указание. Примените теорему косинусов.
Решение. По теореме косинусов из треугольника BKC
находим, что
BK=\sqrt{CK^{2}+CB^{2}-2CK\cdot CB\cos\angle KCB}=\sqrt{9+25-2\cdot3\cdot5\cdot\frac{4}{5}}=\sqrt{10}.
Если R
— радиус окружности, описанной около треугольника BKC
, то
R=\frac{BK}{2\sin\angle KCB}=\frac{\sqrt{10}}{2\cdot\frac{3}{5}}=\frac{5\sqrt{10}}{6}.
По теореме косинусов из треугольника ABC
находим, что
AB=\sqrt{AC^{2}+BC^{2}-2AC\cdot BC\cos\angle ACB}=\sqrt{16+25-2\cdot4\cdot5\cdot\frac{4}{5}}=3.
Следовательно, треугольник BAK
— прямоугольный (BK^{2}=10=1+9=AK^{2}+AB^{2})
. Поэтому радиус окружности, вписанной в этот треугольник, можно вычислить по формуле (см. задачу 217)
r=\frac{AB+AK-BK}{2},~\mbox{т. е.}~r=\frac{4-\sqrt{10}}{2}.
Следовательно,
\frac{R}{r}=\frac{5\sqrt{10}}{3(4-\sqrt{10})}=\frac{10\sqrt{10}+25}{9}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1975, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 180
