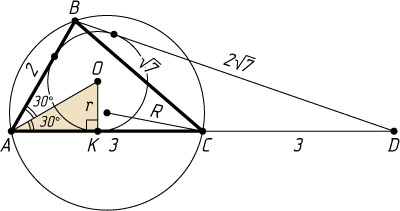
923. В треугольнике ABC
косинус угла BAC
равен \frac{1}{2}
, AB=2
, AC=3
. Точка D
лежит на продолжении стороны AC
, причём C
находится между A
и D
, CD=3
. Найдите отношение радиуса окружности, описанной около треугольника ABC
, к радиусу окружности, вписанной в треугольник ABD
.
Ответ. \frac{7+4\sqrt{7}}{9}
.
Указание. Примените теорему косинусов.
Решение. По теореме косинусов из треугольника ABC
находим, что
BC=\sqrt{AB^{2}+AC^{2}-2AB\cdot AC\cos\angle BAC}=\sqrt{4+9-6}=\sqrt{7}.
Если R
— радиус окружности, описанной около треугольника ABC
, то
R=\frac{BC}{2\sin\angle BAC}=\frac{\sqrt{7}}{\sqrt{3}}.
По теореме косинусов из треугольника ABD
находим, что BD=2\sqrt{7}
. Пусть O
— центр окружности, вписанной в этот треугольник, r
— её радиус, K
— точка касания со стороной AD
. Тогда
r=OK=AK\tg\angle OAK=\left(\frac{AB+BD+AD}{2}-BD\right)\tg30^{\circ}=\frac{4-\sqrt{7}}{\sqrt{3}}
(см. задачу 219). Следовательно, \frac{R}{r}=\frac{7+4\sqrt{7}}{9}
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1975, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 180
