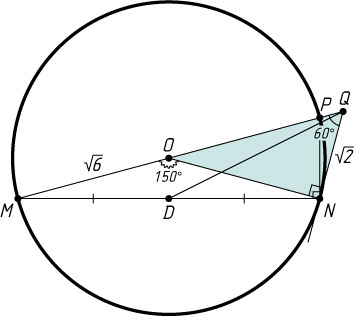
936. В окружности радиуса R=\sqrt{6}
проведены хорда MN
и диаметр MP
. В точке N
проведена касательная к окружности, которая пересекает продолжение диаметра MP
в точке Q
под углом 60^{\circ}
. Найдите медиану QD
треугольника MQN
.
Ответ. \sqrt{5\pm\frac{5\sqrt{3}}{2}}
.
Решение. Пусть O
— центр окружности. Предположим, что точка Q
лежит на продолжении диаметра MP
за точку P
(рис. 1). Из прямоугольного треугольника ONQ
находим, что
QN=ON\cdot\ctg60^{\circ}=\sqrt{6}\cdot\frac{\sqrt{3}}{3}=\sqrt{2},~OQ=2NQ=2\sqrt{2}.
Тогда QM=MO+OQ=\sqrt{6}+2\sqrt{2}
. По теореме о внешнем угле треугольника
\angle MON=90^{\circ}+60^{\circ}=150^{\circ}.
По теореме косинусов из равнобедренного треугольника MON
находим, что
MN^{2}=OM^{2}+ON^{2}-2OM\cdot ON\cos150^{\circ}=6+6+2\cdot6\cdot\frac{\sqrt{3}}{2}=12+6\sqrt{3}.
По формуле для медианы треугольника (см. задачу 4014)
QD^{2}=\frac{1}{4}(2QN^{2}+2QM^{2}-MN^{2})=\frac{1}{4}\left(2\cdot2+2(\sqrt{6}+2\sqrt{2})^{2}-12-6\sqrt{3}\right)=
=\frac{1}{4}(20+10\sqrt{3}).
Следовательно,
QD=\frac{1}{2}\sqrt{20+10\sqrt{3}}=\sqrt{5+\frac{5\sqrt{3}}{2}}.
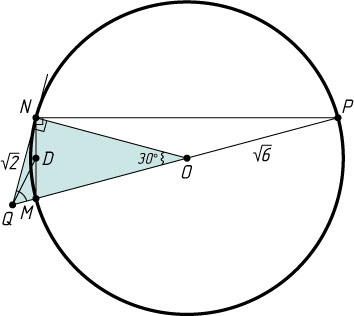
Если точка Q
лежит на продолжении диаметра MP
за точку M
(рис. 2), то аналогично получим, что QD=\sqrt{5-\frac{5\sqrt{3}}{2}}
.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1986, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 26

