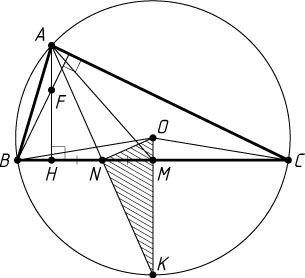
939. В треугольнике ABC
проведены высота AH
, равная h
, медиана AM
, равная m
, и биссектриса AN
. Точка N
— середина отрезка MH
. Найдите расстояние от вершины A
до точки пересечения высот треугольника ABC
.
Ответ. \frac{m^{2}-h^{2}}{2h}
.
Указание. Расстояние от вершины треугольника до точки пересечения высот вдвое больше расстояния от центра описанной окружности до стороны, противолежащей данной вершине.
Решение. Из прямоугольных треугольников AHM
и AHN
находим, что
HM^{2}=AM^{2}-AH^{2}=m^{2}-h^{2},~HN=\frac{1}{2}HM=\frac{\sqrt{m^{2}-h^{2}}}{2},
AN^{2}=AH^{2}+HN^{2}=h^{2}+\frac{m^{2}-h^{2}}{4}=\frac{m^{2}+3h^{2}}{4}.
Пусть O
— центр окружности, описанной около треугольника ABC
, K
— отличная от A
точка пересечения прямой AN
с описанной окружностью. Поскольку AK
— биссектриса угла BAC
, то \cup BK=\cup KC
. Поэтому OK
— биссектриса угла BOC
равнобедренного треугольника BOC
. Следовательно, точка M
лежит на OK
. Поэтому KM\perp BC
, а так как NH=NM
, то из равенства прямоугольных треугольников AHN
и KMN
следует, что AN=NK
. Поэтому ON\perp AK
.
В прямоугольном треугольнике ONK
известно, что NK=AN
, KM=AH=h
. Тогда
NK^{2}=OK\cdot KM,~\mbox{или}~\frac{m^{2}+3h^{2}}{4}=(h+OM)h.
Отсюда находим, что
OM=\frac{m^{2}-h^{2}}{4h}.
Пусть F
— точка пересечения высот треугольника ABC
. Тогда (см. задачу 1257)
AF=2OM=\frac{m^{2}-h^{2}}{2h}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1986, вариант 1, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 44
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.21, с. 123
