942. Через центр O
окружности, описанной вокруг остроугольного треугольника ABC
, проведена прямая, перпендикулярная BO
и пересекающая отрезок AB
в точке P
и продолжение отрезка BC
за точку C
в точке Q
. Найдите BP
, если известно, что AB=c
, BC=a
и BQ=p
.
Ответ. \frac{ap}{c}
.
Указание. Докажите, что треугольники ABC
и QBP
подобны.
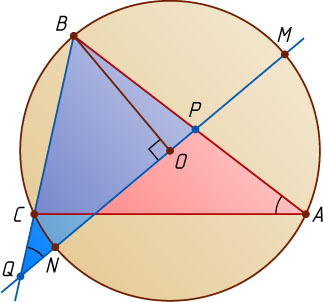
Решение. Пусть прямая PQ
пересекает описанную окружность в точках M
и N
(N
расположена между P
и Q
). Тогда
\smile MB=\smile NB,~\angle BAC=\frac{1}{2}\smile BC=\frac{1}{2}(\smile NB-\smile NC)=
=\frac{1}{2}(\smile MB-\smile NC)=\angle MQB
(см. задачу 27). Следовательно, треугольники ABC
и QBP
подобны по двум углам. Поэтому \frac{BC}{BP}=\frac{AB}{BQ}
. Отсюда находим, что
BP=\frac{BC\cdot BQ}{AB}=\frac{ap}{c}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1991, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.25, с. 113
