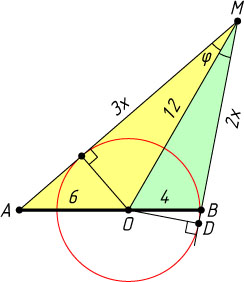
963. Точка O
делит отрезок AB
на отрезки OA=6
и OB=4
. С центром в точке O
проведена окружность, из A
и B
к ней проведены касательные, пересекающиеся в точке M
, причём точки касания лежат по разные стороны от прямой AB
. Найдите радиус окружности, если OM=12
.
Ответ. \frac{6\sqrt{21}}{7}
.
Указание. Примените теорему косинусов к треугольникам AMO
и BMO
.
Решение. Первый способ. Поскольку MO
— биссектриса угла AMB
, то
\frac{AM}{MB}=\frac{AO}{OB}=\frac{3}{2}.
Обозначим AM=3x
, BM=2x
, \angle AMB=2\varphi
. По теореме косинусов из треугольников AMO
и BMO
находим, что
AO^{2}=AM^{2}+MO^{2}-2AM\cdot MO\cos\varphi,
BO^{2}=MB^{2}+MO^{2}-2MB\cdot MO\cos\varphi,
или
36=9x^{2}+144-72x\cos\varphi,~16=4x^{2}+144-48x\cos\varphi,
или
24x\cos\varphi=3x^{2}+36,~24x\cos\varphi=2x^{2}+64.
Вычитая почленно полученные равенства, получим, что x^{2}=28
. Тогда
\cos\varphi=\frac{5}{2\sqrt{7}},~\sin\varphi=\frac{\sqrt{3}}{2\sqrt{7}}.
Пусть D
— точка касания данной окружности со стороной BM
. Тогда
OD=OM\sin\varphi=\frac{12\sqrt{3}}{2\sqrt{7}}=\frac{6\sqrt{21}}{7}.
Второй способ. Поскольку MO
— биссектриса угла AMB
, то
\frac{AM}{MB}=\frac{AO}{OB}=\frac{3}{2}.
(см. задачу 1509). Обозначим MA=3x
, MB=2x
. По формуле для квадрата биссектрисы треугольника, MO^{2}=MA\cdot MB-OA\cdot OB
(см. задачу 791), или 144=6x^{2}-24
. Отсюда находим, что x=2\sqrt{7}
. Тогда MA=3x=6\sqrt{7}
, MB=2x=4\sqrt{7}
.
По формуле Герона
S_{\triangle AMB}=\sqrt{(5\sqrt{7}+5)(5\sqrt{7}-5)(5-\sqrt{7})(5+\sqrt{7})}=4\sqrt{6\cdot18}=30\sqrt{3}.
С другой стороны, если радиус окружности равен r
, то
S_{\triangle AMB}=S_{\triangle AMO}+S_{\triangle BMO}=\frac{1}{2}AM\cdot r+\frac{1}{2}BM\cdot r=\frac{1}{2}r(6\sqrt{7}+4\sqrt{7})=5r\sqrt{7}.
Из уравнения 5r\sqrt{7}=30\sqrt{3}
находим, что r=\frac{6\sqrt{21}}{7}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1988 (отделение геофизики), вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 122
