966. В треугольнике ABC
на сторонах AB
и AC
выбраны соответственно точки B_{1}
и C_{1}
, причём AB_{1}:AB=1:3
и AC_{1}:AC=1:2
. Через точки A
, B_{1}
и C_{1}
проведена окружность. Через точку B_{1}
проведена прямая, пересекающая отрезок AC_{1}
в точке D
, а окружность — в точке E
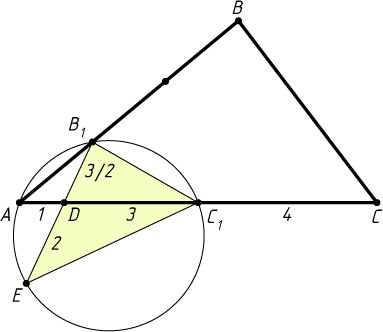
. Найдите площадь треугольника B_{1}C_{1}E
, если AC_{1}=4
, AD=1
, DE=2
, а площадь треугольника ABC
равна 12.
Ответ. \frac{7}{2}
.
Указание. Примените теорему об отрезках пересекающихся хорд.
Решение. По теореме о произведении отрезков пересекающихся хорд
B_{1}D\cdot DE=AD\cdot DC_{1}.
Следовательно,
B_{1}D=AD\cdot\frac{DC_{1}}{DE}=1\cdot\frac{3}{2}=\frac{3}{2}.
Поэтому (см. задачу 3007)
S_{\triangle B_{1}C_{1}E}=\frac{B_{1}E}{BD}S_{\triangle B_{1}DC_{1}}=\frac{7}{3}S_{\triangle B_{1}DC_{1}}=
=\frac{7}{3}\cdot\frac{DC_{1}}{AC_{1}}S_{\triangle AB_{1}C_{1}}=\frac{7}{3}\cdot\frac{3}{4}S_{\triangle AB_{1}C_{1}}=
=\frac{7}{4}S_{\triangle AB_{1}C_{1}}=\frac{7}{4}\cdot\frac{AB_{1}}{AB}\cdot\frac{AC_{1}}{AC}S_{\triangle ABC}=\frac{7}{4}\cdot\frac{1}{3}\cdot\frac{1}{2}\cdot12=\frac{7}{2}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1988, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 177
