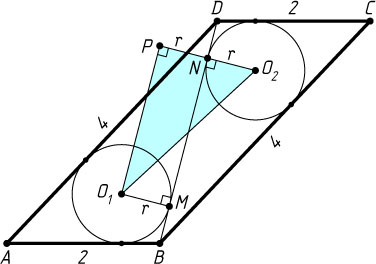
988. В параллелограмме со сторонами 2 и 4 проведена диагональ, равная 3. В каждый из получившихся треугольников вписано по окружности. Найдите расстояние между центрами окружностей.
Ответ. \frac{\sqrt{51}}{3}
.
Указание. Найдите радиусы окружностей (площадь треугольника, делённая на полупериметр).
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники ABD
и BDC
, BD
— диагональ параллелограмма ABCD
, BD=3
, AB=2
, BC=4
.
Треугольники ABD
и BDC
равны по трём сторонам, следовательно, равны и радиусы вписанных в них окружностей. Обозначим эти радиусы через r
, полупериметры — через p
. Тогда
S_{\triangle ABD}=S_{\triangle BDC}=\sqrt{p(p-AB)(p-AD)(p-BD)}=
=\sqrt{\frac{9}{2}\cdot\frac{5}{2}\cdot\frac{1}{2}\cdot\frac{3}{2}}=\frac{3\sqrt{15}}{4}.
Тогда
r=\frac{S_{\triangle ABD}}{p}=\frac{\sqrt{15}}{6}.
Пусть M
и N
— точки касания первой и второй окружностей с диагональю BD
. Тогда
DN=BM=p-AD=\frac{9}{2}-4=\frac{1}{2}
(см. задачу 219). Поэтому MN=BD-2BM=3-1=2
.
Пусть P
— проекция центра O_{1}
на прямую O_{2}N
. Тогда
O_{2}P=O_{2}N+NP=O_{2}N+O_{1}M=2r=\frac{\sqrt{15}}{3}.
По теореме Пифагора из прямоугольного треугольника O_{1}PO_{2}
находим, что
O_{1}O_{2}=\sqrt{O_{1}P^{2}+O_{2}P^{2}}=\sqrt{MN^{2}+O_{2}P^{2}}=\sqrt{4+\frac{15}{9}}=\frac{\sqrt{51}}{3}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1970, № 3, вариант 1
