995. Докажите, что четыре окружности, описанные около четырёх треугольников, образованных четырьмя пересекающимися прямыми плоскости, имеют общую точку (точка Микеля).
Решение. Первый способ. Пусть прямые AB
, AC
и BC
пересекают четвёртую прямую в точках D
, E
и F
соответственно.
Пусть P
— точка пересечения окружностей, описанных около треугольников ABC
и CEF
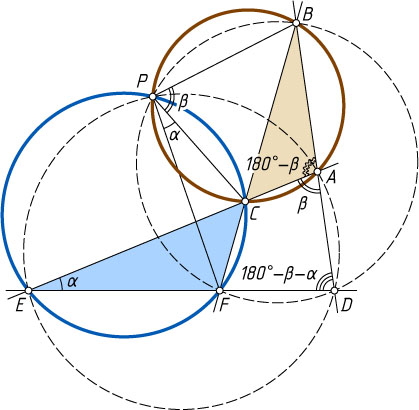
. Рассмотрим случай, изображённый на рисунке 1. Обозначим \angle CPF=\alpha
, \angle BPC=\beta
. Тогда
\angle BPF=\alpha+\beta,~\angle AED=\angle CEF=\angle CPF=\alpha,
\angle BAE=\angle BAC=180^{\circ}-\angle BPC=180^{\circ}-\beta,
а так как BAE
— внешний угол треугольника DAE
, то
\angle BDF=\angle BDE=\angle BAE-\angle AED=180^{\circ}-\beta-\alpha.
Значит, сумма углов при противоположных вершинах P
и D
четырёхугольника DBPF
равна 180^{\circ}
. Поэтому точка P
лежит на окружности, описанной около треугольника BDF
. Аналогично докажем, что точка P
лежит на окружности, описанной около треугольника ADE
.
Аналогично для любого другого расположения четырёх прямых, образующих четыре треугольника.
Второй способ. Рассмотрим случай, изображённый на рисунке 2. Центр поворотной гомотетии, переводящей отрезок CE
в отрезок BD
, есть отличная от A
точка O
пересечения описанных окружностей треугольников ADE
и ABC
(см. задачу 5599), а центр поворотной гомотетии, переводящей отрезок BC
в отрезок DE
, есть отличная от F
точка O'
пересечения описанных окружностей треугольников CFE
и BFD
. Точки O
и O'
совпадают (см. задачу 6440), следовательно, все четыре окружности проходят через точку O
. Что и требовалось доказать.
Примечание. Разбор случаев не нужен, если рассматривать ориентированные углы.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 157, с. 46; № 167(1), с. 47
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 64, с. 107
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 22
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 4, с. 200
Источник: Польские математические олимпиады. — 1960, задача 6
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 72, с. 21
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.83(а), с. 40
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.88(а), с. 40; № 19.46, с. 393
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 256, с. 68
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 553, с. 68
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 78
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 56
