10131. В треугольнике ABC
угол A
равен \alpha
, BC=a
. Вписанная окружность касается прямых AB
и AC
в точках M
и P
. Найдите длину хорды, высекаемой на прямой MP
окружностью с диаметром BC
.
Ответ. a\sin\frac{\alpha}{2}
.
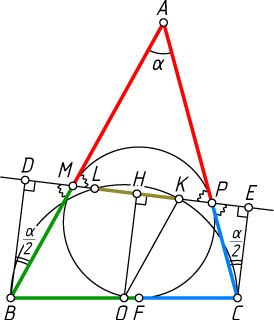
Решение. Первый способ. Пусть O
— середина стороны BC
, т. е. центр окружности с диаметром BC
, отрезки BD
, CE
и OH
— перпендикуляры к прямой MP
, а K
и L
— точки пересечения этой окружности с прямой MP
, F
точка касания вписанной окружности треугольника ABC
со стороной BC
.
Углы при основании MP
равнобедренного треугольника AMP
равны
\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}.
Из прямоугольного треугольника BMD
находим, что
BD=BM\sin\angle BMD=BF\sin\angle AMP=BF\sin\left(90^{\circ}-\frac{\alpha}{2}\right)=BF\cos\frac{\alpha}{2}.
Аналогично, CE=CF\cos\frac{\alpha}{2}
.
Отрезок OH
— средняя линия прямоугольной трапеции (или прямоугольника, если треугольник ABC
равнобедренный) BDEC
, поэтому
OH=\frac{1}{2}(BD+CE)=\frac{1}{2}BF\cos\frac{\alpha}{2}+\frac{1}{2}CF\cos\frac{\alpha}{2}=\frac{1}{2}(BF+CF)\cos\frac{\alpha}{2}=
=\frac{1}{2}BC\cos\frac{\alpha}{2}=\frac{a}{2}\cos\frac{\alpha}{2}.
Из прямоугольного треугольника OHK
находим, что
HK=\sqrt{OK^{2}-OH^{2}}=\sqrt{OB^{2}-OH^{2}}=\sqrt{\left(\frac{a}{2}\right)^{2}-\left(\frac{a}{2}\cos\frac{\alpha}{2}\right)^{2}}=
=\frac{a}{2}\sqrt{1-\cos^{2}\frac{\alpha}{2}}=\frac{a}{2}\sin\frac{\alpha}{2}.
Следовательно,
KL=2HK=a\sin\frac{\alpha}{2}.
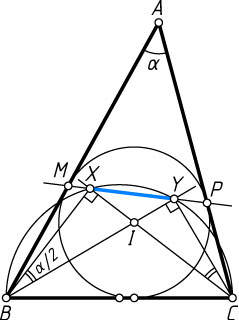
Второй способ. Пусть I
— центр вписанной окружности треугольника ABC
, X
и Y
— точки пересечения прямых соответственно BI
и CI
с прямой MP
. Тогда
\angle BXC=\angle CYB=90^{\circ}
(см. задачу 58). Значит, точки X
и Y
лежат на окружности с диаметром BC
, поэтому XY
— искомая хорда. При этом по теореме о внешнем угле треугольника
\angle XCY=\angle BIC-\angle IXC=\left(90^{\circ}+\frac{\alpha}{2}\right)-90^{\circ}=\frac{\alpha}{2}.
Следовательно, по теореме синусов
XY=BC\sin\angle XCY=a\sin\frac{\alpha}{2}.
Автор: Шарыгин И. Ф.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2005, I, финал, задача 4, 8 класс
Источник: Всероссийская олимпиада по геометрии. — 2005, 11 класс

