10140. Две равные окружности пересекаются в точках A
и B
; P
— отличная от A
и B
точка одной из окружностей; X
и Y
— вторые точки пересечения прямых PA
и PB
с другой окружностью. Докажите, что прямая, проходящая через точку P
и перпендикулярная AB
, делит одну из дуг XY
пополам.
Решение. Рассмотрим случай, когда точка P
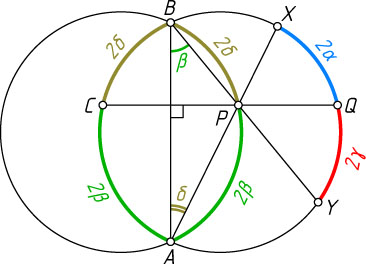
лежит внутри одной из окружностей (см. рисунок). Для остальных случаев рассуждения аналогичны.
Пусть точка P
первой окружности лежит внутри второй окружности, CQ
— хорда второй окружности, проходящая через точку P
перпендикулярно AB
, причём точка C
лежит внутри первой окружности.
Положим
\smile QX=2\alpha,~\smile AC=\smile AP=2\beta,
\smile QY=2\gamma,~\smile BC=\smile BP=2\delta.
Тогда (см. задачу 26)
\angle QPX=\frac{\smile QX+\smile AC}{2}=\alpha+\beta,
\angle QPY=\frac{\smile QY+\smile BC}{2}=\gamma+\delta.
В то же время, учитывая что фигура, состоящая из равных пересекающихся окружностей, симметрична относительно их общей хорды, получим
\beta-\delta=\frac{1}{2}\smile AP-\frac{1}{2}\smile BP=
=\angle PBA-\angle PAB=(90^{\circ}-\angle BPC)-(90^{\circ}-\angle APC)=
=\angle APC-\angle BPC=\angle QPX-\angle QPY=(\alpha+\beta)-(\gamma+\delta),
откуда \alpha=\gamma
. Следовательно, Q
— середина дуги XQY
. Что и требовалось доказать.
Автор: Заславский А. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2006, II, финал, задача 4, 8 класс
Источник: Всероссийская олимпиада по геометрии. — 2006, 8 класс
