10235. Точка E
— середина боковой стороны CD
трапеции ABCD
. На стороне AB
отмечена точка K
так, что CK\parallel AE
. Отрезки CK
и BE
пересекаются в точке O
.
а) Докажите, что CO=KO
.
б) Найдите отношение оснований BC
и AD
, если площадь треугольника BCK
составляет \frac{9}{64}
площади трапеции.
Ответ. 3:5
.
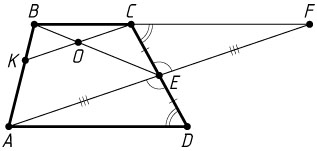
Решение. а) Пусть прямые AE
и BC
пересекаются в точке F
. Треугольники FEC
и AED
равны по стороне (CE=DE
) и двум прилежащим к ней углам. Значит, AE=EF
, т. е. BE
— медиана треугольника ABF
, а так как CK\parallel AF
, то BO
— медиана треугольника KBC
(см. задачу 2607), т. е. O
— середина отрезка KC
.
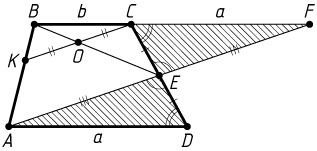
б) Обозначим AD=a
, BC=b
. Из равенства треугольников FEC
и AED
следует, что треугольник ABF
равновелик трапеции ABCD
. Значит, площадь треугольника KBC
составляет \frac{9}{64}
площади подобного ему треугольника ABF
. Тогда коэффициент подобия равен \frac{3}{8}
, т. е.
\frac{3}{8}=\frac{BC}{BF}=\frac{BC}{BC+CF}=\frac{b}{b+a},
откуда \frac{1}{1+\frac{a}{b}}=\frac{3}{8}
. Из этого равенства находим, что \frac{a}{b}=\frac{5}{3}
.
Источник: ЕГЭ. — 2017, 2 июня

