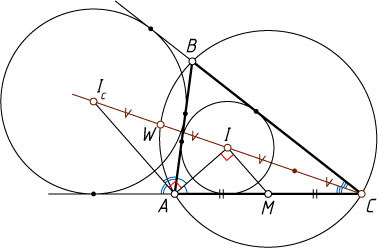
10316. Точка I
— центр вписанной окружности треугольника ABC
, точка M
— середина стороны AC
, а точка W
— середина дуги AB
описанной окружности, не содержащей C
. Оказалось, что \angle AIM=90^{\circ}
. В каком отношении точка I
делит отрезок CW
?
Ответ. 2:1
.
Решение. Пусть I_{c}
— центр вневписанной окружности, касающейся стороны AB
. Поскольку AI
и AI_{c}
— биссектрисы смежных углов, AI_{c}\perp AI
. Значит, IM\parallel AI_{c}
, т. е. IM
— средняя линия треугольника ACI_{c}
. Точки C
, I
, W
и I_{c}
лежат на биссектрисе угла ACB
. По теореме Мансиона (см. задачу 57) точка W
— середина отрезка II_{c}
. Следовательно, CI=II_{c}=2IW
.
Примечание. 1. Верно и обратное: если CI=2IW
, или CI=II_{c}
, то \angle AIM=90^{\circ}
.
Действительно, по теореме Мансиона W
— середина отрезка II_{c}
, значит, IM
— средняя линия треугольника ACI_{c}
, поэтому IM\parallel I_{c}A
, а так как \angle IAI_{c}=90^{\circ}
, то \angle AIM=90^{\circ}
.
2. См. статью А.Заславского «Приключения одной задачи», Квант, 2017, N12, с.19-21.
Автор: Берлов С. Л.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2017, XIII, финальный тур, № 2, 9 класс
Источник: Журнал «Квант». — 2017, № 12, с. 19
Источник: Вступительный экзамен на математико-механический факультет ЛГУ (СПбГУ). —
