1045. Внутри треугольника ABC
взята точка P
так, что \angle PAC=\angle PBC
. Из точки P
на стороны BC
и CA
опущены перпендикуляры PM
и PK
соответственно. Пусть D
— середина стороны AB
. Докажите, что DK=DM
.
Указание. Докажите равенство треугольников KED
и DFM
, где E
и F
— середины AP
и BP
.
Решение. Пусть \angle PAC=\angle PBC=\alpha
. Если E
и F
— середины AP
и BP
соответственно, то \angle KEP=\angle MFP=2\alpha
. Поскольку DE
и DF
— средние линии треугольника APB
, то DEPF
— параллелограмм, а так как медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), то
KE=EP=DF~\mbox{и}~ED=FP=FM,
\angle KED=2\alpha+\angle PED=2\alpha+\angle PFD=\angle MFD.
Поэтому треугольники KED
и DFM
равны по двум сторонам и углу между ними. Следовательно, DK=DM
.
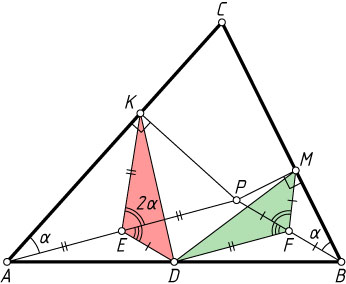
Источник: Австралийские математические олимпиады. — 1983
Источник: Журнал «Crux Mathematicorum». — 1986, № 2, задача 2, с. 22
