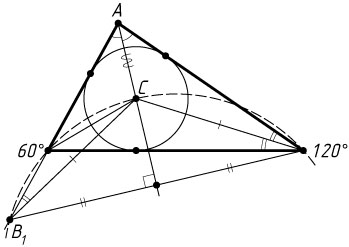
10475. Точка O
— центр окружности, вписанной в треугольник ABC
, в котором AC\lt BC
. Точка B_{1}
симметрична точке B
относительно прямой OC
.
а) Докажите, что точки A
, B
, O
и B_{1}
лежат на одной окружности.
б) Найдите площадь четырёхугольника AOBB_{1}
, если AB=10
, AC=6
, BC=8
.
Ответ. 18.
Решение. а) Центр окружности, вписанной в треугольник, — точка пересечения его биссектрис, поэтому луч CO
— биссектриса угла ACB
. Значит, точка B_{1}
, симметричная точке B
относительно прямой CO
, лежит на луче CA
, а так как CB_{1}=CB\gt AC
, то B_{1}
лежит на продолжении стороны CA
за точку A
, причём CB_{1}=CB
.
Треугольники OB_{1}C
и OBC
равны по двум сторонам и углу между ними, поэтому
\angle OB_{1}A=\angle OB_{1}C=\angle OBC=\angle OBA.
Из точек B
и B_{1}
, лежащих по одну сторону от прямой OA
, отрезок OA
виден под одним и тем же углом, следовательно, точки A
, B
, O
и B_{1}
лежат на одной окружности (см. задачу 12).
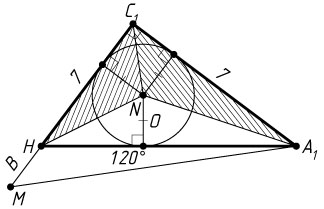
б) Поскольку AB^{2}=AC^{2}+BC^{2}
, треугольник ABC
прямоугольный с прямым углом при вершине C
, значит,
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\cdot6\cdot8=24.
Пусть r
— радиус окружности, вписанной в треугольник ABC
. Полупериметр p
треугольника ABC
равен 12, поэтому
r=\frac{S_{\triangle ABC}}{p}=\frac{24}{12}=2.
Тогда
S_{\triangle AOC}=\frac{1}{2}AC\cdot r=\frac{1}{2}\cdot6\cdot2=6,
S_{\triangle BOC}=\frac{1}{2}BC\cdot r=\frac{1}{2}\cdot8\cdot2=8.
Следовательно,
S_{AOBB_{1}}=S_{\triangle B_{1}BC}-S_{\triangle AOC}-S_{\triangle BOC}=32-6-8=18.
Источник: ЕГЭ. — 2017

