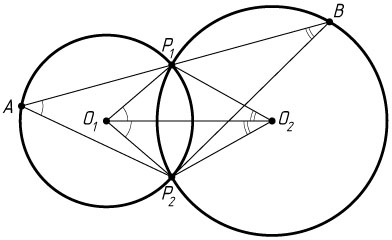
10480. Две окружности с центрами O_{1}
и O_{2}
и радиусами 3 и 4 пересекаются в точках A
и B
, причём точки O_{1}
и O_{2}
лежат по разные стороны от прямой AB
. Через точку A
проведена прямая, вторично пересекающая эти окружности в точках M
и K
, причём точка A
лежит между точками M
и K
.
а) Докажите, что треугольники MBK
и O_{1}AO_{2}
подобны.
б) Найдите расстояние от точки B
до прямой MK
, если MK=7
, а O_{1}O_{2}=5
.
Ответ. \frac{84}{25}
.
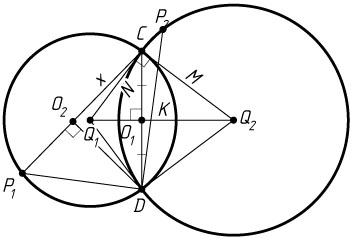
Решение. а) Пусть точка M
лежит на меньшей окружности с центром O_{1}
. Вписанный в эту окружность угол AMB
вдвое меньше центрального угла AO_{1}B
, а значит, равен углу AO_{1}O_{2}
. Аналогично, \angle AKB=\angle AO_{2}O_{1}
. Следовательно, треугольники MBK
и O_{1}AO_{2}
подобны по двум углам.
б) Линия центров пересекающихся окружностей перпендикулярна их общей хорде и делит её пополам, поэтому отрезок AB
вдвое больше высоты AH
треугольника AO_{1}O_{2}
. Этот треугольник прямоугольный, так как
O_{1}A^{2}+O_{2}A^{2}=3^{2}+4^{2}=5^{2}=O_{1}O_{2}^{2}.
Значит,
AH=\frac{O_{1}A\cdot O_{2}A}{O_{1}O_{2}}=\frac{3\cdot4}{5}=\frac{12}{5}
(см. задачу 1967).
Расстояние от точки B
до прямой MK
равно высоте BP
треугольника MBK
. Коэффициент подобия треугольников MBK
и O_{1}AO_{2}
равен \frac{MK}{O_{1}O_{2}}=\frac{7}{5}
, а отрезок BP
при этом подобии соответствует отрезку AH
. Следовательно,
BP=\frac{7}{5}AH=\frac{7}{5}\cdot\frac{12}{5}=\frac{84}{25}.
Источник: ЕГЭ. — 2017

