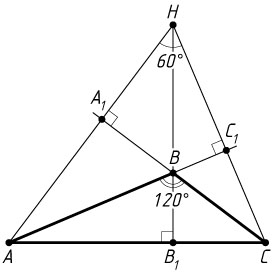
10492. Высоты треугольника ABC
с тупым углом ABC
пересекаются в точке H
. Угол AHC
равен 60^{\circ}
.
а) Докажите, что угол ABC
равен 120^{\circ}
.
б) Найдите BH
, если AB=6
, BC=10
.
Ответ. \frac{14}{\sqrt{3}}
.
Решение. а) Пусть AA_{1}
и CC_{1}
— высоты треугольника ABC
. Поскольку угол ABC
тупой, точка H
пересечения прямых AA_{1}
и CC_{1}
лежит вне треугольника ABC
. При этом точки B
и H
лежат по одну сторону от прямой AC
.
В четырёхугольнике BA_{1}HC_{1}
углы при вершинах A_{1}
и C_{1}
равны по 90^{\circ}
, значит, сумма двух других углов этого четырёхугольника равна 180^{\circ}
. Следовательно,
\angle ABC=\angle A_{1}BC_{1}=180^{\circ}-\angle AHC=180^{\circ}-60^{\circ}=120^{\circ}.
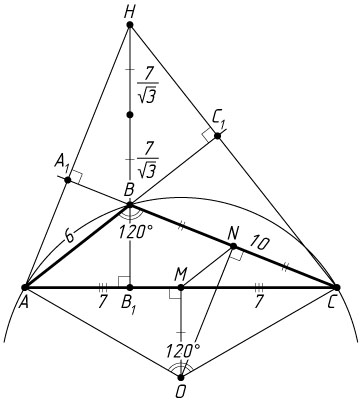
б) Пусть O
— центр окружности, описанной около треугольника ABC
, M
— середина стороны AC
. Известно, что BH=2OM
(см. задачу 1257).
(Действительно, если N
— середина стороны BC
, то MN
— средняя линия треугольника ABC
, значит, MN\parallel AB
. Прямая ON
— серединный перпендикуляр к стороне BC
, а так как AH\perp BC
, то ON\parallel AH
. Прямые OM
и BH
также параллельны, т. е. обе они перпендикулярны прямой AC
. Значит, стороны треугольника ABH
соответственно параллельны сторонам треугольника NOM
. Эти треугольники подобны с коэффициентом 2, так как AB=2MN
. Следовательно, BH=2OM
.)
Поскольку угол ABC
тупой, точки H
и O
лежат по разные стороны от прямой AC
. Градусная мера дуги AC
, не содержащей точки B
, вдвое больше градусной меры вписанного угла ABC
, т. е. равна 240^{\circ}
. Тогда градусная мера дуги ABC
равна 120^{\circ}
. Значит, соответствующий этой дуге центральный угол AOC
также равен 120^{\circ}
.
По теореме косинусов
AC=\sqrt{BA^{2}+BC^{2}-2BA\cdot BC\cos120^{\circ}}=\sqrt{36+100+6\cdot10}=\sqrt{196}=14.
Из прямоугольного треугольника OMC
находим, что
OM=CM\ctg\angle COM=7\ctg60^{\circ}=\frac{7}{\sqrt{3}}.
Следовательно,
BH=2OM=\frac{14}{\sqrt{3}}.
Источник: ЕГЭ. — 2018, досрочный экзамен, 30 марта

