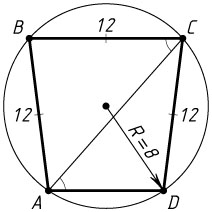
10509. Четырёхугольник вписан в окружность радиуса R=8
. Известно, что AB=BC=CD=12
.
а) Докажите, что прямые BC
и AD
параллельны.
б) Найдите AD
.
Ответ. 9.
Решение. а) Вписанные углы CAD
и ACB
опираются на равные хорды CD
и AB
, поэтому \angle ACB=\angle CAD
. Следовательно, BC\parallel AD
.
б) Обозначим \angle CAD=\angle BAC=\alpha
. Треугольник ACD
вписан в окружность радиуса R
. По теореме синусов
\sin\alpha=\frac{CD}{2R}=\frac{12}{16}=\frac{3}{4}.
Тогда
\cos\angle ADC=\cos2\alpha=1-2\sin^{2}\alpha=1-2\cdot\frac{7}{16}=-\frac{1}{8}\lt0.
Значит, углы при основании AD
равнобокой трапеции ABCD
— тупые.
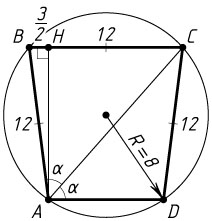
Пусть AH
— высота трапеции. Тогда точка H
лежит на отрезке BC
. Из прямоугольного треугольника AHB
находим, что
AB\cos(180^{\circ}-2\alpha)=-12\cos2\alpha=-12\cdot\left(-\frac{1}{8}\right)=\frac{3}{2}.
С другой стороны (см. задачу 1921),
CH=\frac{BC-AD}{2}=\frac{12-AD}{2}.
Из уравнения \frac{12-AD}{2}=\frac{3}{2}
находим, что AD=9
.
Источник: ЕГЭ. — 2018, 1 июня

