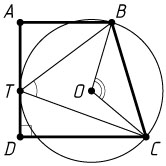
10515. Окружность с центром O
, расположенным внутри прямоугольной трапеции ABCD
, проходит через вершины B
и C
большей боковой стороны и касается боковой стороны AD
в точке T
.
а) Докажите, что угол BOC
вдвое больше угла BTC
.
б) Найдите расстояние от точки T
до прямой BC
, если основания трапеции AB
и CD
равны 4 и 9 соответственно.
Ответ. 6
.
Указание. См. задачу 117.
Решение. а) Точки O
и T
расположены по одну сторону от прямой BC
, поэтому центральный угол, соответствующий вписанному углу BTC
, — это угол BOC
. Следовательно, \angle BOC=2\angle BTC
.
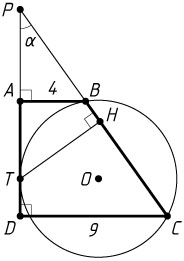
б) Пусть продолжения боковых сторон трапеции пересекаются в точке P
, а H
— основание перпендикуляра, опущенного из точки T
на боковую сторону BC
. Обозначим \angle DPC=\alpha
. Из прямоугольных треугольников PDC
, PHT
и PAB
получаем, что
\sin\alpha=\frac{CD}{PC},~\sin\alpha=\frac{TH}{PT},~\sin\alpha=\frac{AB}{PB}.
Значит, \frac{CD}{PC}=\frac{TH}{PT}
и \frac{AB}{PB}=\frac{TH}{PT}
. Перемножив эти два равенства, получим, что
\frac{TH^{2}}{PT^{2}}=\frac{CD\cdot AB}{PC\cdot PB},
а так как по теореме о касательной и секущей PT^{2}=PC\cdot PB
, то
TH^{2}=CD\cdot AB=4\cdot9=36.
Следовательно, TH=6
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2018

