10516. Точка O
— центр окружности, описанной около остроугольного треугольника ABC
, а BH
— высота этого треугольника.
а) Докажите, что углы ABH
и CBO
равны.
б) Найдите BH
, если AB=16
, BC=18
, BH=BO
.
Ответ. 12
.
Указание. См. задачу 20.
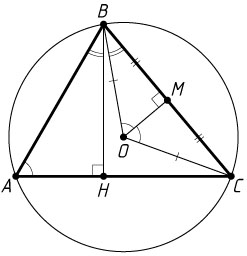
Решение. а) Пусть OM
— перпендикуляр, опущенный из центра окружности на сторону BC
. Тогда M
— середина основания BC
равнобедренного треугольника BOC
. Поскольку треугольник ABC
остроугольный, центр O
его описанной окружности лежит внутри треугольника. Значит, BOC
— центральный угол, соответствующий вписанному углу BAC
, поэтому
\angle BAC=\frac{1}{2}\angle BOC=\angle BOM.
Два угла прямоугольного треугольника AHB
соответственно равны двум углам прямоугольного треугольника BMO
, значит, третьи углы этих треугольников также равны, т. е.
\angle ABH=\angle MBO=\angle CBO.
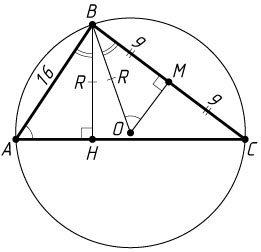
б) Обозначим BH=BO=R
. Прямоугольные треугольники AHB
и BMO
подобны по двум углам, поэтому \frac{BH}{AB}=\frac{BM}{BO}
, или \frac{R}{16}=\frac{9}{R}
. Отсюда находим, что
R^{2}=9\cdot16=144=12^{2}.
Следовательно, BH=R=12
.
Источник: ЕГЭ. — 2018

