1062. На сторонах AB
и BC
треугольника ABC
как на гипотенузах построены вне его прямоугольные треугольники APB
и BQC
с одинаковыми углами величины \beta
при их общей вершине B
. Найдите углы треугольника PQK
, где K
— середина стороны AC
.
Ответ. 180^{\circ}-2\beta
; \beta
; \beta
.
Указание. Пусть M
и N
— середины AB
и BC
. Докажите равенство треугольников KNQ
и PMK
.
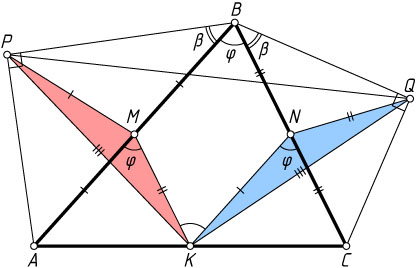
Решение. Обозначим \angle ABC=\varphi
. Рассмотрим случай, когда \varphi+2\beta\lt180^{\circ}
(рис. 1). Пусть M
и N
— середины сторон AB
и BC
треугольника ABC
. Тогда (см. задачу 1109)
KN=\frac{1}{2}AB=PM,~KM=\frac{1}{2}BC=QN,
\angle KNQ=\angle KNC+\angle CNQ=\varphi+2\beta,~\angle KMP=\angle KMA+\angle AMP=\varphi+2\beta.
Следовательно, треугольники KNQ
и PMK
равны по двум сторонам и углу между ними. Поэтому треугольник PQK
— равнобедренный. Тогда
\angle PKQ=\angle PKM+\angle MKN+\angle NKQ=\varphi+\angle PKM+\angle NKQ=
=\varphi+\angle PKM+\angle MPK=\varphi+180^{\circ}-\angle PMK=
=\varphi+180^{\circ}-(\varphi+2\beta)=180^{\circ}-2\beta;
\angle QPK=\angle PQK=\beta.
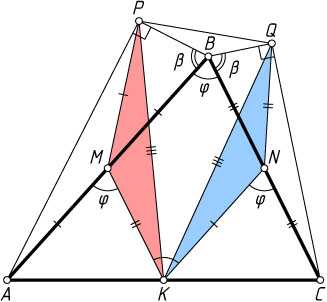
Аналогично для случая, когда \varphi+2\beta\geqslant180^{\circ}
(рис. 2).
Автор: Купцов Л. П.
Источник: Всероссийская олимпиада школьников. — 1976-77, III, IV этап, 10 класс
Источник: Журнал «Квант». — 1983, № 5, с. 42, М802
Источник: Задачник «Кванта». — М802

