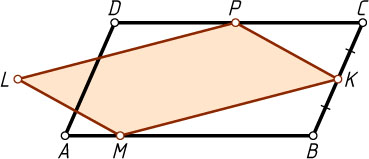
10690. Вершины M
, K
и P
параллелограмма MKPL
расположены на сторонах соответственно AB
, BC
и CD
параллелограмма ABCD
, причём K
— середина стороны BC
(см. рис.). Докажите, что диагональ одного из этих параллелограммов проходит через точку пересечения диагоналей другого.
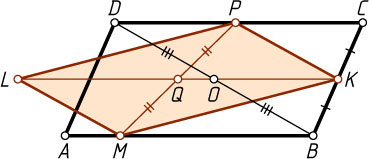
Решение. Первый способ. Пусть O
— центр параллелограмма ABCD
. Тогда O
— середина отрезка BD
, поэтому KO
— средняя линия треугольника CBD
. Значит, KO\parallel AB
.
Пусть Q
— точка пересечения диагоналей параллелограмма MKPL
. Тогда KQ
— средняя линия трапеции MBCP
. Значит, KQ\parallel AB
. Следовательно, прямые KO
и KL
совпадают, т. е. диагональ KL
параллелограмма MKPL
проходит через точку пересечения диагоналей параллелограмма ABCD
.
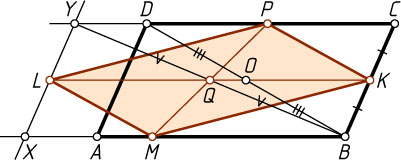
Второй способ. Через точку L
проведём прямую, параллельную BC
. Пусть эта прямая пересекает прямые AB
и CD
в точках X
и Y
. Тогда XBCY
— параллелограмм, причём вершины параллелограмма MKPL
лежат по одной сторонах параллелограмма XBCY
. Тогда точка Q
пересечения диагоналей параллелограмма MKPL
(середина KL
) совпадает с точкой пересечения диагоналей параллелограмма XBCY
(см. задачу 1057), т. е. с серединой его диагонали BY
. Значит, KQ\parallel CY
как средняя линия треугольника BCY
.
С другой стороны, по теореме Фалеса прямая KQ
проходит через середину отрезка BD
, т. е. через центр параллелограмма ABCD
.
Источник: Московская устная олимпиада по геометрии. — 2018, № 1, 8-9 классы


