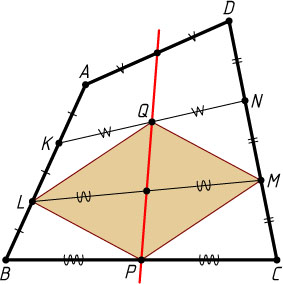
1071. На стороне AB
четырёхугольника ABCD
отмечены точки K
и L
, а на стороне CD
— точки M
и N
. При этом AK=KL=LB
и CM=MN=ND
. Докажите, что середины отрезков LM
, KN
и середины сторон BC
и AD
лежат на одной прямой.
Указание. Середины сторон любого четырёхугольника образуют параллелограмм.
Решение. Пусть P
и Q
— середины отрезков BC
и KN
соответственно. Тогда LPMQ
— параллелограмм (см. задачу 1204). Его диагонали LM
и PQ
делятся точкой пересечения пополам. Следовательно, середины BC
, LM
и KN
лежат на одной прямой. Аналогично докажем, что на этой прямой лежит и середина стороны AD
.