10742. Окружность радиуса 1 касается внешним образом вписанной окружности \omega
треугольника ABC
и сторон AB
и AC
. Окружность радиуса 4 касается внешним образом окружности \omega
и сторон AB
и BC
. Окружность радиуса 9 касается внешним образом окружности \omega
и сторон AC
и BC
. Найдите радиус окружности \omega
.
Ответ. 11.
Решение. Обозначим BC=a
, AC=b
, AB=c
, p
— полупериметр треугольника ABC
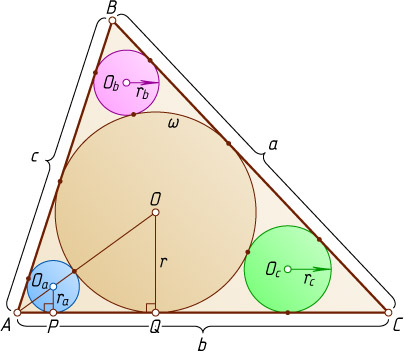
. Пусть O_{a}
, O_{b}
и O_{c}
— центры указанных в условии окружностей радиусов r_{a}=1
, r_{b}=4
и r_{c}=9
соответственно, O
— центр окружности \omega
искомого радиуса r
, P
и Q
— точки касания окружностей радиуса r_{a}
и r
со стороной AC
соответственно.
Тогда AQ=p-a
(см. задачу 219) и PQ=2\sqrt{rr_{1}}
(см. задачу 365). Из подобия прямоугольных треугольников APO_{a}
и AQO
получаем
\frac{r_{a}}{r}=\frac{AP}{AQ}=\frac{AQ-PQ}{AQ}=1-\frac{PQ}{AQ}=1-\frac{2\sqrt{r_{1}r}}{p-a},
откуда
p-a=\frac{2r\sqrt{rr_{a}}}{r-r_{a}}=\frac{2r\sqrt{r}}{r-1}.
Аналогично,
p-b=\frac{2r\sqrt{rr_{b}}}{r-r_{b}}=\frac{4r\sqrt{r}}{r-4},~p-c=\frac{2r\sqrt{rr_{c}}}{r-r_{c}}=\frac{6r\sqrt{r}}{r-9}.
Пусть S
— площадь треугольника ABC
. Тогда S=pr
, а по формуле Герона
S^{2}=p(p-a)(p-b)(p-c)=p^{2}r^{2},
поэтому
(p-a)(p-b)(p-c)=r^{2}p,
или
(p-a)(p-b)(p-c)=r^{2}(p-a+p-b+p-c).
Подставив в это равенство выражения
p-a=\frac{2r\sqrt{r}}{r-1},~p-b=\frac{4r\sqrt{r}}{r-4},~p-c=\frac{6r\sqrt{r}}{r-9},
получим
\frac{48r^{4}\sqrt{r}}{(r-1)(r-4)(r-9)}=2r^{3}\sqrt{r}\left(\frac{1}{r-1}+\frac{2}{r-4}+\frac{3}{r-9}\right)~\Leftrightarrow
\Leftrightarrow~24r=(r-4)(r-9)+2(r-1)(r-9)+3(r-1)(r-4)~\Leftrightarrow
\Leftrightarrow~r^{2}-12r+11=0~\Leftrightarrow~(r-1)(r-11)=0.
Условию задачи удовлетворяет корень r=11
.
Источник: Журнал «Crux Mathematicorum». — 1987, № 10, задача 75 (1985, с. 105), с. 318