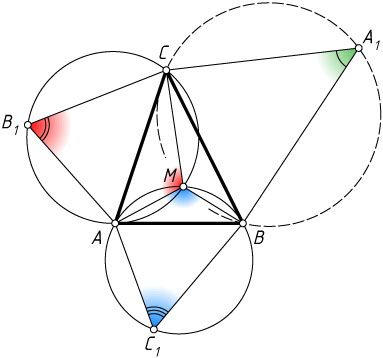
1081. На сторонах треугольника ABC
внешним образом построены подобные треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
, Докажите, что описанные окружности построенных треугольников пересекаются в одной точке. (В построенных подобных треугольниках углы при вершинах A_{1}
, B_{1}
, C_{1}
не являются соответственными.)
Указание. Докажите, что точка пересечения окружностей, описанных около двух из указанных треугольников, лежит на окружности, описанной около третьего. Рассмотрите все возможные случаи.
Решение. Поскольку углы при вершинах A_{1}
, B_{1}
, C_{1}
построенных треугольников не являются соответственными, их сумма равна 180^{\circ}
.
Обозначим через M
точку пересечения окружностей, описанных около треугольников AC_{1}B
и ACB_{1}
, отличную от A
, и докажем, что точка M
лежит на окружности, описанной около треугольника A_{1}BC
.
Пусть точка лежит внутри треугольника ABC
. Тогда
\angle BMC=360^{\circ}-\angle AMB-\angle AMC=
=360^{\circ}-(180^{\circ}-\angle AC_{1}B)-(180^{\circ}-\angle AB_{1}C)=\angle AC_{1}B+\angle AB_{1}C,
поэтому
\angle BMC+\angle BA_{1}C=\angle AC_{1}B+\angle AB_{1}C+\angle BA_{1}C=180^{\circ}.
Следовательно, точки B
, A_{1}
, M
, C
лежат на одной окружности, т. е. все три окружности проходят через точку M
.
Аналогично для остальных случаев.
Примечание. Это частный случай следующего более общего утверждения. Если на сторонах треугольника ABC
внешним образом построены треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
, причём сумма их углов при вершинах A_{1}
, B_{1}
и C_{1}
равна 180^{\circ}
, то описанные окружности построенных треугольников пересекаются в одной точке.
В частности, если треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
равносторонние, то их описанные окружности пересекаются в одной точке — точке Торичелли (см. задачу 6703).