10810. Дан треугольник ABC
. Точки D
, E
и F
лежат на прямых BC
, AC
и AB
соответственно, причём прямые AD
, BE
и CF
пересекаются в точке O
. Точки F
, B
, C
и E
лежат на одной окружности. Точки A
, F
, D
и C
тоже лежат на одной окружности. Докажите, что AD
, BE
и CF
— высоты треугольника ABC
.
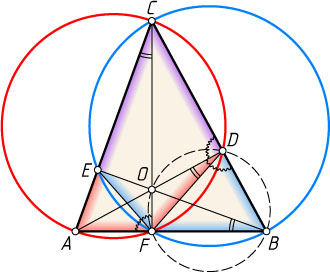
Решение. Докажем это утверждение для остроугольного треугольника (см. рис.). С небольшими изменениями доказательство годится для тупоугольного и прямоугольного.
Из вписанных четырёхугольников ACDF
и FECB
получаем
\angle ADF=\angle ACF=\angle ECF=\angle EBF=\angle EBA,
поэтому
\angle ODF=\angle ADF=\angle EBA=\angle EBA=\angle OBF.
Значит, четырёхугольник ODBF
тоже вписанный (см. задачу 12). Тогда
\angle AFC=\angle BDO,
а так как
\angle ADC=\angle AFC=\angle BDO~\mbox{и}~\angle ADC+\angle BDO=180^{\circ},
то
\angle ADC=\angle BDO=\angle AFC=90^{\circ}.
Значит, AD
и CF
— высоты треугольника ABC
, а O
— его ортоцентр. Следовательно, BE
— третья высоты треугольника ABC
. Утверждение доказано.
Примечание. Верно также следующее утверждение. Если точка P
лежит на высоте CF
треугольника ABC
, а прямые AP
и BP
пересекают стороны BC
и AC
в точках D
и E
соответственно, то \angle PFD=\angle PFE
(см. задачу 1206).
Источник: Журнал «Crux Mathematicorum». — 1987, № 8, задача 1155 (1986, с. 140), с. 268; 2010, № 4, задача 6, с. 231
Источник: Австралийские математические олимпиады. — 2005
