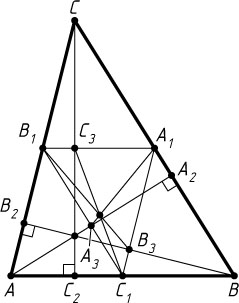
1086. AA_{1}
, BB_{1}
и CC_{1}
— медианы треугольника ABC
, AA_{2}
, BB_{2}
и CC_{2}
— высоты, A_{3}
, B_{3}
и C_{3}
— середины соответствующих высот. Докажите, что прямые, A_{1}A_{3}
, B_{1}B_{3}
и C_{1}C_{3}
пересекаются в одной точке.
Решение. Точки A_{3}
, B_{3}
и C_{3}
лежат на средних линиях B_{1}C_{1}
, A_{1}C_{1}
и A_{1}B_{1}
треугольника ABC
, причём
\frac{B_{1}A_{3}}{A_{3}C_{1}}=\frac{BA_{2}}{A_{2}C},~\frac{A_{1}B_{3}}{B_{3}C_{1}}=\frac{CB_{2}}{B_{2}A},~\frac{B_{1}C_{3}}{C_{3}A_{1}}=\frac{AC_{2}}{C_{2}B}.
Поэтому
\frac{A_{1}B_{3}}{B_{3}C_{1}}\cdot\frac{C_{1}A_{3}}{A_{3}B_{1}}\cdot\frac{B_{1}C_{3}}{C_{3}A_{1}}=\frac{CB_{2}}{B_{2}A}\cdot\frac{BA_{2}}{A_{2}C}\cdot\frac{AC_{2}}{C_{2}B}=\frac{CB_{2}}{B_{2}A}\cdot\frac{AC_{2}}{C_{2}B}\cdot\frac{BA_{2}}{A_{2}C}.
Прямые, содержащие высоты треугольника, пересекаются в одной точке, поэтому по теореме Чевы (см. задачу 1621) \frac{CB_{2}}{B_{2}A}\cdot\frac{AC_{2}}{C_{2}B}\cdot\frac{BA_{2}}{A_{2}C}=1
. Значит, \frac{A_{1}B_{3}}{B_{3}C_{1}}\cdot\frac{C_{1}A_{3}}{A_{3}B_{1}}\cdot\frac{B_{1}C_{3}}{C_{3}A_{1}}=1
. Следовательно, прямые A_{1}A_{3}
, B_{1}B_{3}
и C_{1}C_{3}
пересекаются в одной точке.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 9.6, с. 72
