1087. Через точку M
, лежащую вне окружности, проведены касательные MA
, MB
(A
и B
— точки касания) и секущие MCD
и MEF
. Докажите, что прямые CF
, DE
и AB
пересекаются в одной точке.
Решение. Рассмотрим случай, когда точка C
лежит между M
и D
, а точка E
— между M
и F
.
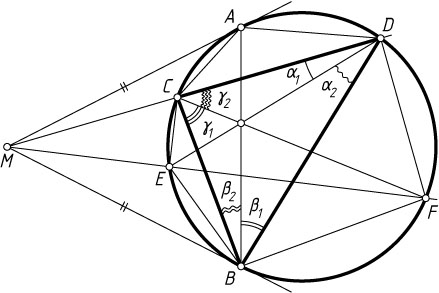
Обозначим
\angle CDE=\alpha_{1},~\angle BDE=\alpha_{2},
\angle DBA=\beta_{1},~\angle ABC=\beta_{2},
\angle FCB=\gamma_{1},~\angle DCF=\gamma_{2}.
Пусть радиус окружности равен R
. По теореме синусов
\sin\alpha_{1}=\frac{CE}{2R},~\sin\alpha_{2}=\frac{BE}{2R},
\sin\beta_{1}=\frac{AD}{2R},~\sin\beta_{2}=\frac{AC}{2R},
\sin\gamma_{1}=\frac{BF}{2R},~\sin\gamma_{2}=\frac{DF}{2R}.
Треугольник MAC
подобен треугольнику MDA
, треугольник MCE
— треугольнику MFD
, а треугольник MEB
— треугольнику MBF
, поэтому
\frac{AD}{AC}=\frac{MD}{MA},~\frac{CE}{DF}=\frac{ME}{MD},~\frac{BF}{BE}=\frac{MB}{ME},
а так как MA=MB
, то после почленного перемножения трёх равенств получим, что
\frac{AD}{AC}\cdot\frac{CE}{DF}\cdot\frac{BF}{BE}=\frac{MD}{MA}\cdot\frac{ME}{MD}\cdot\frac{MB}{ME}=\frac{MB}{MA}=1.
Значит,
\frac{\sin\alpha_{1}}{\sin\alpha_{2}}\cdot\frac{\sin\beta_{1}}{\sin\beta_{2}}\cdot\frac{\sin\gamma_{1}}{\sin\gamma_{2}}=\frac{\frac{CE}{2R}}{\frac{BE}{2R}}\cdot\frac{\frac{AD}{2R}}{\frac{AC}{2R}}\cdot\frac{\frac{BF}{2R}}{\frac{DF}{2R}}=\frac{CE}{BE}\cdot\frac{AD}{AC}\cdot\frac{BF}{DF}=\frac{AD}{AC}\cdot\frac{CE}{DF}\cdot\frac{BF}{BE}=1.
Следовательно, по теореме Чевы (в тригонометрической форме), применённой к треугольнику DBC
, прямые CF
, DE
и AB
пересекаются в одной точке (см. задачу 1900).
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 70
