10876. Пусть AA_{1}
и BB_{1}
— высоты остроугольного неравнобедренного треугольника ABC
, M
— середина стороны AB
, а касательные, проведённые в точках A
и B
к описанной окружности треугольника ABC
, пересекают прямую A_{1}B_{1}
в точках X
и Y
соответственно и пересекаются в точке Z
. Докажите, что M
— центр вписанной окружности треугольника XYZ
.
Решение. Треугольник AZB
равнобедренный с основанием AB
, поэтому его медиана ZM
является биссектрисой. Следовательно, ZM
— биссектриса угла при вершине Z
треугольника XYZ
.
Отрезок B_{1}M
— медиана прямоугольного треугольника ABB_{1}
, проведённая из вершины прямого угла, поэтому MA=MB_{1}
(см. задачу 1109). Значит, точка M
лежит на серединном перпендикуляре к отрезку AB_{1}
.
Из равенства углов CB_{1}A_{1}
и ABC
(см. задачу 141) и из теоремы об угле между касательной и хордой следует, что
\angle AB_{1}X=\angle CB_{1}A_{1}=\angle ABC=\angle XAB_{1},
Значит, треугольник AXB_{1}
равнобедренный, XA=XB_{1}
, т. е. точка X
также лежит на серединном перпендикуляре к отрезку AB_{1}
. Тогда XM
— биссектриса угла при вершине X
треугольника XYZ
.
Следовательно, M
— точка пересечения биссектрис этого треугольника, т. е. центр его вписанной окружности. Что и требовалось доказать.
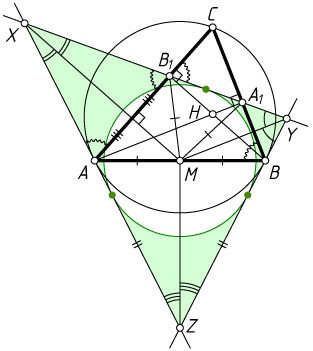
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Источник: Журнал «Квант». — 2014, № 1, с. 44
