10877. Пусть AA_{1}
и BB_{1}
— высоты остроугольного неравнобедренного треугольника ABC
, M
— середина стороны AB
, а касательные, проведённые в точках A
и B
к описанной окружности треугольника ABC
, пересекают прямую A_{1}B_{1}
в точках X
и Y
соответственно. Докажите, что окружности, описанные около треугольников AMA_{1}
и BMB_{1}
, проходят через точки X
и Y
соответственно.
Решение. Из теоремы об угле между касательной и хордой следует, что
\angle XAB_{1}=\angle XAC=\angle ABC.
Поскольку
\angle AB_{1}X=\angle CB_{1}A_{1}=\angle ABC
(см. задачу 141), треугольник AXB_{1}
равнобедренный, а XM
— биссектриса угла при его вершине X
(см. задачу 10876). Значит,
\angle MXA_{1}=\angle MXB_{1}=90^{\circ}-\angle AB_{1}X=90^{\circ}-\angle ABC=
=90^{\circ}-\angle ABA_{1}=\angle BAA_{1}=\angle MAA_{1}.
Из точек X
и A
, лежащих по одну сторону от прямой MA_{1}
, отрезок MA_{1}
виден под одним и тем же углом, следовательно, точки A
, M
, A_{1}
и X
лежат на одной окружности — описанной окружности треугольника AMA_{1}
.
Аналогично, точка Y
лежит на описанной окружности треугольника BMB_{1}
.
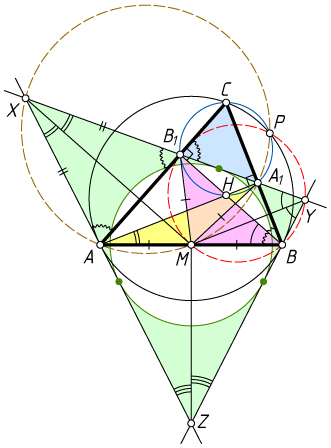
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Блинков Ю. А.
Источник: Журнал «Квант». — 2014, № 1, с. 45
