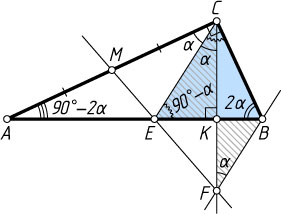
1091. Из вершины C
прямого угла прямоугольного треугольника ABC
опущена высота CK
, и в треугольнике ACK
проведена биссектриса CE
. Прямая, проходящая через точку B
параллельно CE
, пересекает прямую CK
в точке F
. Докажите, что прямая EF
делит отрезок AC
пополам.
Решение. Обозначим \angle KCE=\angle ACE=\alpha
. Тогда
\angle ABC=\angle ACK=2\alpha,~\angle BAC=90^{\circ}-2\alpha,~\angle BEC=\alpha+(90^{\circ}-2\alpha)=90^{\circ}-\alpha=\angle BCE,
значит, треугольник BCE
— равнобедренный, BE=BC
.
Из подобия треугольников CKE
и FKB
следует, что \frac{KE}{KB}=\frac{CK}{KF}
, поэтому \frac{CF}{FK}=\frac{BE}{BK}=\frac{BC}{BK}
.
По свойству биссектрисы треугольника \frac{KE}{EA}=\frac{CK}{AC}=\cos2\alpha=\frac{BK}{BC}
.
Пусть прямая FE
пересекает отрезок AC
в точке M
. По теореме Менелая (см. задачу 1622) для треугольника AKC
получаем, что \frac{KE}{EA}\cdot\frac{AM}{MC}\cdot\frac{CF}{FK}=1
, или \frac{BK}{BC}\cdot\frac{AM}{MC}\cdot\frac{BC}{BK}=1
. Следовательно, \frac{AM}{MC}=1
. Что и требовалось доказать.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.62, с. 112
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.75, с. 110
