10949. На одной стороне прямого угла с вершиной A_{0}
выбрана такая точка B
, что A_{0}B=4
, а на другой стороне выбраны такие точки A_{1}
, A_{2}
, …, что для любого n=1
, 2, \dots
радиус окружности, вписанной в треугольник BA_{n-1}A_{n}
, равен 1. Найдите длину отрезка A_{0}A_{n}
.
Ответ. 2^{n+1}-\frac{1}{2^{n-1}}
.
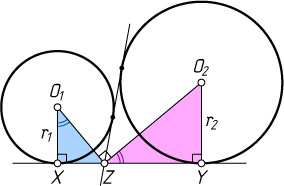
Решение. Лемма 1. Пусть общая внешняя касательная, проведённая к двум непересекающимся окружностям радиусов r_{1}
и r_{2}
, касается их в точках X
и Y
, а общая внутренняя касательная пересекает отрезок XY
в точке Z
(рис. 1). Тогда XZ\cdot YZ=r_{1}r_{2}
.
Доказательство. Пусть O_{1}
и O_{2}
— центры окружностей. Прямоугольные треугольники XO_{1}Z
и YZO_{2}
подобны, так как
\angle XO_{1}Z=90^{\circ}-\angle XZO_{1}=YZO_{2}.
Следовательно, XZ\cdot YZ=r_{1}r_{2}
.
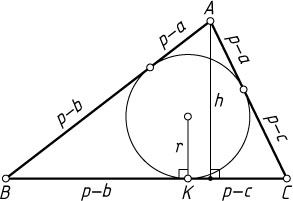
Лемма 2. Пусть в треугольнике ABC
вписанная окружность касается стороны BC
в точке K
(рис. 2). Тогда произведение BK\cdot CK=\frac{r^{2}h}{h-2r}
, где h
— высота, проведённая из вершины A
, а r
— радиус вписанной окружности.
Доказательство. Обозначим a=BC
, b=CA
, c=AB
, p
— полупериметр, S
— площадь треугольника ABC
. Тогда BK=p-b
, CK=p-c
(см. задачу 219), S=pr=\frac{1}{2}ah
, а по формуле Герона,
(p-b)(p-c)=\frac{S^{2}}{p(p-a)}=\frac{pr\cdot ah}{2p(p-a)}=\frac{rh}{2\left(\frac{p}{a}-1\right)}=\frac{rh}{2\left(\frac{h}{2r}-1\right)}=\frac{r^{2}h}{h-2r}.
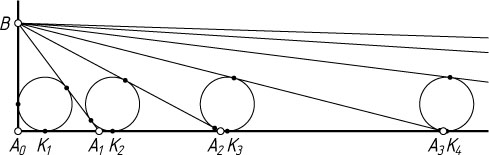
Перейдём к решению задачи (рис. 3). Обозначим через K_{i}
точку касания окружности, вписанной в треугольник BA_{i-1}A_{i}
, со стороной A_{i-1}A_{i}
. Следовательно, K_{i}A_{i}\cdot A_{i}K_{i+1}=1
по лемме 1. У треугольников BA_{i-1}A_{i}
высота, проведённая из вершины B
, равна 4, а радиус вписанной окружности равен 1, значит, A_{i-1}K_{i}\cdot K_{i}A_{i}=2
по лемме 2. Очевидно, A_{0}K_{1}=1
. Поочерёдно пользуясь леммами 2 и 1, получаем, что
K_{1}A_{1}=2,~A_{1}K_{2}=\frac{1}{2},~K_{2}A_{2}=4,~A_{2}K_{3}=\frac{1}{4},~A_{3}K_{3}=8,~\dots,~A_{n-1}K_{n}=\frac{1}{2^{n-1}},~K_{n}A_{n}=2^{n}.
Отсюда
A_{0}A_{n}=(A_{0}K_{1}+A_{1}K_{2}+\dots+A_{n-1}K_{n})+(K_{1}A_{1}+K_{2}A_{2}+\dots+K_{n}A_{n})=
=\left(1+\frac{1}{2}+\dots+\frac{1}{2^{n-1}}\right)+(2+4+\dots+2^{n})=
=\left(2-\frac{1}{2^{n-1}}\right)+(2^{n+1}-2)=2^{n+1}-\frac{1}{2^{n-1}}.
Автор: Расторгуев В. А.
Источник: Журнал «Квант». — 2016, № 2, с. 14, М2415
Источник: Задачник «Кванта». — М2415


