10985. В остроугольном треугольнике ABC
угол A
равен 60^{\circ}
. Высоты BN
и CM
треугольника ABC
пересекаются в точке H
. Точка O
— центр окружности, описанной около треугольника ABC
.
а) Докажите, что AH=AO
.
б) Найдите площадь треугольника AHO
, если BC=6\sqrt{3}
, \angle ABC=45^{\circ}
.
Ответ. 9
.
Решение. а) Из точек M
и N
отрезок AH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AH
. Эта окружность описана около треугольника ANM
. Треугольник ANM
подобен треугольнику ABC
с коэффициентом \cos60^{\circ}=\frac{1}{2}
(см. задачу 19), поэтому её диаметр вдвое меньше диаметра окружности, описанной около треугольника ABC
, т. е. AH=AO
.
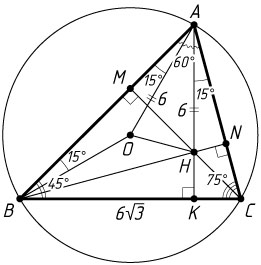
б) Пусть R
— радиус окружности, описанной около треугольника ABC
. По теореме синусов
AH=AO=R=\frac{BC}{2\sin\angle BAC}=\frac{6\sqrt{3}}{2\cdot\frac{\sqrt{3}}{2}}=6.
Пусть AK
— третья высота треугольника ABC
. Из прямоугольного треугольника AKC
находим, что
\angle CAK=90^{\circ}-\angle ACK=90^{\circ}-75^{\circ}=15^{\circ}.
Центральный угол AOB
вдвое больше вписанного угла ACB
, а треугольник AOB
равнобедренный, значит,
\angle BAO=\frac{1}{2}(180^{\circ}-\angle AOB)=\frac{1}{2}(180^{\circ}-2\cdot75^{\circ})=15^{\circ}.
Тогда
\angle OAH=\angle BAC-\angle CAK-\angle BAO=60^{\circ}-15^{\circ}-15^{\circ}=30^{\circ}.
Следовательно,
S_{\triangle AHO}=\frac{1}{2}AH\cdot AO\sin\angle OAH=\frac{1}{2}R^{2}\sin30^{\circ}=\frac{1}{2}\cdot36\cdot\frac{1}{2}=9.
Источник: ЕГЭ. — 2019, 29 мая, задача 16

