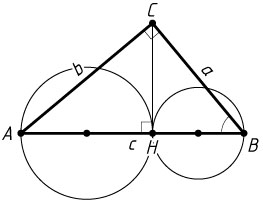
10996. В треугольнике ABC
с прямым углом C
проведена высота CH
. На отрезках AH
и HB
как на диаметрах построены окружности.
а) Докажите, что отношение площадей кругов, построенных на этих диаметрах, равно (\tg\angle ABC)^{4}
.
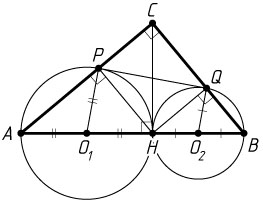
б) Окружность с центром O_{1}
, лежащим на AH
, пересекает отрезок AC
второй раз в точке P
. Окружность с центром O_{2}
, лежащим на HB
, пересекает отрезок BC
второй раз в точке Q
. Найдите площадь четырёхугольника PO_{1}O_{2}Q
, если AC=12
, BC=10
.
Ответ. 30
.
Решение. а) Обозначим BC=a
, AC=b
, AB=c
, S_{1}
и S_{2}
— площади кругов с диаметрами AH
и BH
соответственно. Тогда (см. задачу 2728)
AH=\frac{b^{2}}{c},~BH=\frac{a^{2}}{c},
следовательно,
\frac{S_{1}}{S_{2}}=\frac{\pi\left(\frac{1}{2}AH\right)^{2}}{\pi\left(\frac{1}{2}BH\right)^{2}}=\frac{\left(\frac{1}{2}\cdot\frac{b^{2}}{c}\right)^{2}}{\left(\frac{1}{2}\cdot\frac{a^{2}}{c}\right)^{2}}=\left(\frac{b}{a}\right)^{4}=\left(\frac{AC}{BC}\right)^{4}=(\tg\angle ABC)^{4}
б) Точка P
лежит на окружности с диаметром AH
, поэтому HP\perp AC
. Аналогично HQ\perp BC
. Значит, CPHQ
— прямоугольник, а S_{\triangle PHQ}=\frac{1}{2}S_{CPHQ}
.
Отрезки O_{1}P
и O_{2}Q
— медианы треугольников APH
и BQH
, поэтому
S_{\triangle O_{1}PH}=\frac{1}{2}S_{\triangle APH},~S_{\triangle O_{2}QH}=\frac{1}{2}S_{\triangle BQH}.
Следовательно,
S_{PO_{1}O_{2}Q}=S_{\triangle PHQ}+S_{\triangle O_{1}PH}+S_{\triangle O_{2}QH}=
=\frac{1}{2}S_{CPHQ}+\frac{1}{2}S_{\triangle APH}+\frac{1}{2}S_{\triangle BQH}=
=\frac{1}{2}(S_{CPHQ}+S_{\triangle APH}+S_{\triangle BQH})=
=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}\cdot\frac{1}{2}BC\cdot AC=\frac{1}{4}\cdot10\cdot12=30.
Источник: ЕГЭ. — 2019, 24 июня, резервный день, задача 16

