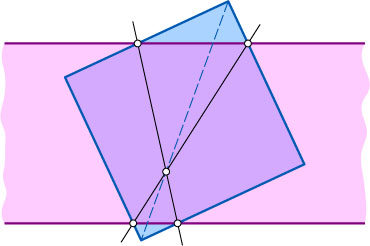
11185. На полосу положили квадрат, сторона которого равна ширине полосы, притом так, что его граница пересекла границу полосы в четырёх точках (см.рисунок). Докажите, что две прямые, проходящие накрест через эти точки, пересекаются на диагонали квадрата.
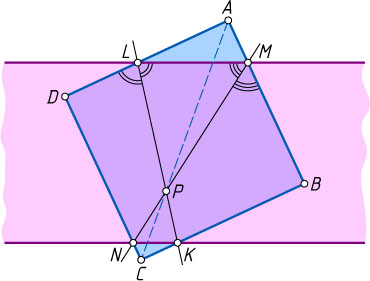
Решение. Пусть стороны AB
и AD
квадрата ABCD
пересекают одну границу полосы в точках M
и L
соответственно, стороны BC
и CD
пересекают вторую границу полосы в точках K
и N
соответственно, а отрезки MN
и KL
пересекаются в точке P
.
Поскольку сторона квадрата равна ширине полосы, точка N
равноудалена от сторон угла BML
. Значит, MN
— биссектрисе этого угла (см. задачу 1138). Аналогично, LK
— биссектриса угла DLM
. Тогда точка P
пересечения MN
и LK
равноудалена от сторон AB
и AD
, значит, она лежит на биссектрисе угла BAD
. Следовательно, точка P
лежит на диагонали AC
квадрата. Что и требовалось доказать.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 2004, № 3, с. 17, М1906; 2004, № 6, с. 19, М1906
Источник: Задачник «Кванта». — 2004, № 3, М1906

