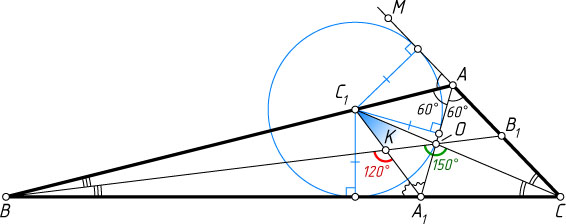
1121. В треугольнике ABC
с углом A
, равным 120^{\circ}
, биссектрисы AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке O
. Докажите, что \angle A_{1}C_{1}O=30^{\circ}
.
Указание. Докажите, что A_{1}C_{1}
— биссектриса угла AA_{1}B
и примените формулу для угла между биссектрисами треугольника (см. задачу 1101).
Решение. Пусть M
— точка на продолжении стороны CA
за точку A
. Тогда луч AB
— биссектриса угла MAA_{1}
(\angle MAB=\angle A_{1}AB=60^{\circ}
). Поэтому расстояния от точки C_{1}
до прямых AC
и AA_{1}
равны между собой. Кроме того, так как точка C_{1}
лежит на биссектрисе угла ACB
, то равны также расстояния от точки C_{1}
до прямых AC
и BC
. Следовательно, точка C_{1}
удалена на равные расстояния от сторон угла AA_{1}B
. Значит, она лежит на биссектрисе угла AA_{1}B
.
Если K
— точка пересечения отрезков BB_{1}
и A_{1}C_{1}
, то K
— точка пересечения биссектрис треугольника BAA_{1}
. Поэтому
\angle C_{1}KO=\angle BKA_{1}=90^{\circ}+\frac{1}{2}\angle BAA_{1}=90^{\circ}+30^{\circ}=120^{\circ}
(см. задачу 1101), а так как
\angle BOC=90^{\circ}+\frac{1}{2}\angle BAC=90^{\circ}+60^{\circ}=150^{\circ},
то по теореме о внешнем угле треугольника
\angle A_{1}C_{1}O=\angle BOC-\angle C_{1}KO=150^{\circ}-120^{\circ}=30^{\circ}.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.31, с. 108
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.36, с. 105
